今回は分布の特性値についてです。
特性値とは、確率分布の特性を表すものです。期待値とか、中央値みたいな代表値の他に、分散や相関係数とかも含まれます。
というわけで、復習も兼ねて一つ一つ確認していきます。
代表値(期待値、中央値、最頻値)
連続型確率変数Xの確率密度関数をf(x)とする時、期待値E[X]は
$$E[X] = \int xf(x)dx $$
で表される。
また、中央値は
$$P(x \leq a)=0.5$$
となるxである。
さらにf(x)が最大となるxを最頻値という。
この3つの代表値は、不均衡な分布では異なる値をとる。
一般的に右に裾が長い分布においては、最頻値<中央値<期待値となる
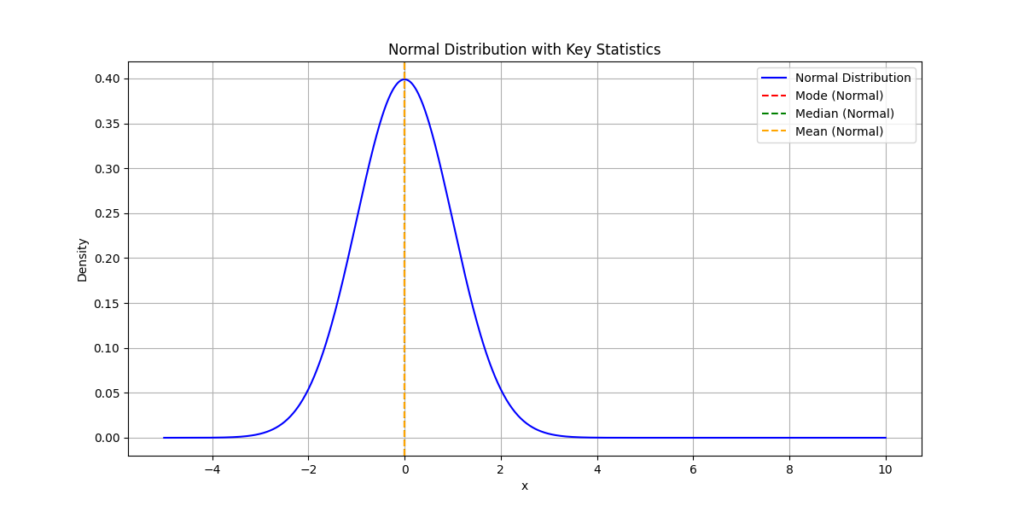
正規分布の確率密度関数。期待値、中央値、最頻値はすべて一致。
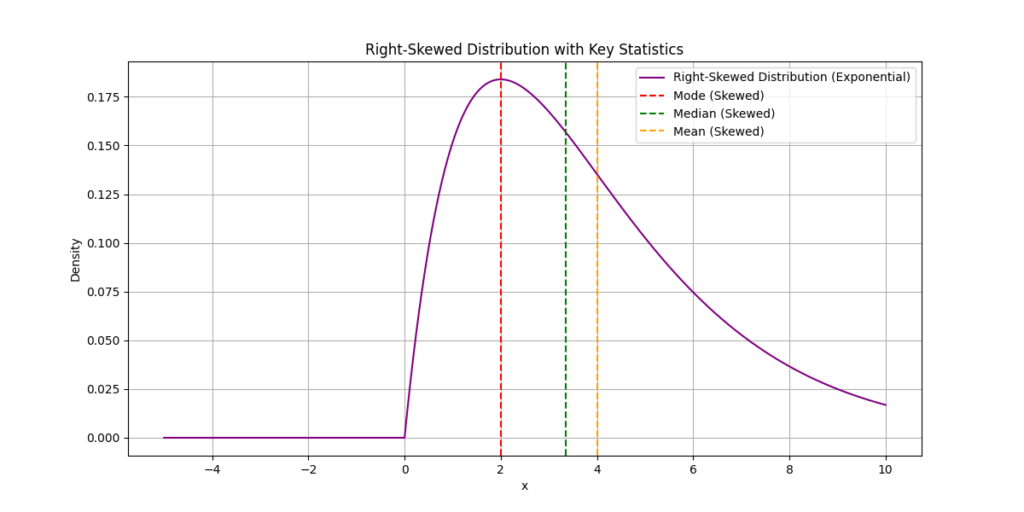
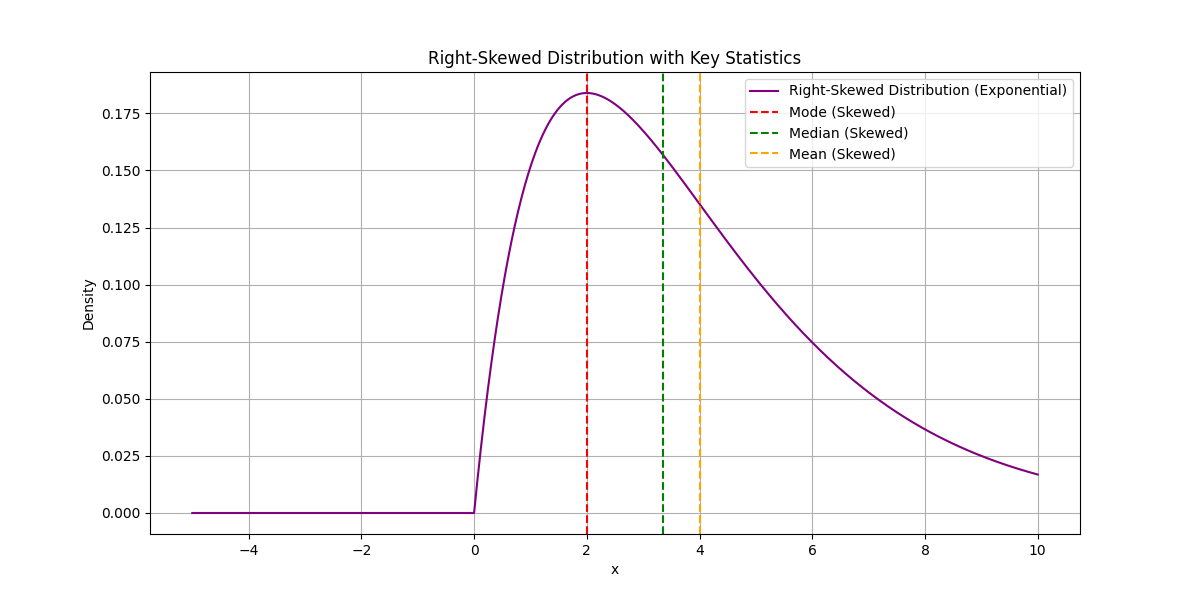
ガンマ分布は正規分布に比べると右に裾が長い。
その場合最頻値<中央値<期待値となっている。
※画像でexponentialと書かれていますがガンマ分布です。(私のコード修正ミスです。)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, gamma
# Define the x-axis range
x = np.linspace(-5, 10, 1000)
# Parameters for the normal distribution
mean_normal = 0
std_normal = 1
pdf_normal = norm.pdf(x, loc=mean_normal, scale=std_normal)
# Parameters for the gamma distribution
shape_gamma = 2 # Shape parameter (k)
scale_gamma = 2 # Scale parameter (theta)
pdf_gamma = gamma.pdf(x, a=shape_gamma, scale=scale_gamma)
# Calculate key statistics for normal distribution
mode_normal = mean_normal # Mode = Mean for normal distribution
median_normal = mean_normal # Median = Mean for normal distribution
mean_normal = mean_normal # Mean is already defined
# Calculate key statistics for gamma distribution
mode_gamma = (shape_gamma - 1) * scale_gamma if shape_gamma > 1 else 0 # Mode for gamma
median_gamma = gamma.median(a=shape_gamma, scale=scale_gamma) # Median for gamma
mean_gamma = shape_gamma * scale_gamma # Mean for gamma
# Plot Normal Distribution
plt.figure(figsize=(12, 6))
plt.plot(x, pdf_normal, label="Normal Distribution", color="blue")
plt.axvline(mode_normal, color="red", linestyle="--", label="Mode (Normal)")
plt.axvline(median_normal, color="green", linestyle="--", label="Median (Normal)")
plt.axvline(mean_normal, color="orange", linestyle="--", label="Mean (Normal)")
plt.title("Normal Distribution with Key Statistics")
plt.xlabel("x")
plt.ylabel("Density")
plt.legend()
plt.grid()
plt.show()
# Plot Right-Skewed Distribution
plt.figure(figsize=(12, 6))
plt.plot(x, pdf_gamma, label="Right-Skewed Distribution (gamma)", color="purple")
plt.axvline(mode_gamma, color="red", linestyle="--", label="Mode (Skewed)")
plt.axvline(median_gamma, color="green", linestyle="--", label="Median (Skewed)")
plt.axvline(mean_gamma, color="orange", linestyle="--", label="Mean (Skewed)")
plt.title("Right-Skewed Distribution with Key Statistics")
plt.xlabel("x")
plt.ylabel("Density")
plt.legend()
plt.grid()
plt.show()
状況に応じて適切な代表値は異なるが、一般則で言えば、外れ値に囚われにくい中央値が優れていると言われている。
標準偏差、四分位範囲、変動係数
標準偏差は
$$\sigma = \sqrt{V[X]}$$
四分位範囲は
$$IQR = (P(x\leq{a})=0.75となるa) – (P(x\leq{b})=0.25となるb)$$
で表されます。
一般的に、裾が長い分布では標準偏差は大きくなりやすいので、四分位範囲を用いることが多い。
また、非負値の確率変数の散らばりの指標としては変動係数
$$\sqrt{V[X]}/E[X]$$
を用いることがある。
変動係数はE[X]で標準偏差を割っていることから確率変数のスケールに依存せず、
複数の確率変数の散らばりを比較する際に有用。
同時確率分布の特性値
2つの確率変数XとYについて、互いに独立でない場合、
分散について加法は成立しない、すなわち、
$$V[X+Y] \neq V[X]+V[Y]$$
である。ここで、
$$V[X+Y]=E{(X-\mu_1)+(X-\mu_2)}^2$$
なので、これを展開して計算すると、
$$V[X+Y]=V[X]+V[Y]+2E{(X-\mu_1)(X-\mu_2)}$$
このおまけみたいな\(V[X+Y]=V[X]+V[Y]+2E{(X-\mu_1)(X-\mu_2)}\)を共分散Cov(X, Y)という
なお、\(Cov(X, Y) = E[XY]-E[X]E[Y]\)である。
また、共分散をそれぞれの標準偏差の積で割った値
$$\rho_{xy} = \frac{Cov(X, Y)}{\sqrt{V[X]}\sqrt{V[Y]}}$$
を相関係数という。
偽相関と偏相関係数
2つの確率変数X、Yが別の確率変数Xによってそれぞれ影響を受けている場合、
XとYは見かけ上相関があるようにみえる。
例:アイスクリームが売れると溺死事故が増える
→暑い日にはアイスクリームが売れ、また暑い日に海やプールで泳ぐ人が増えるため。アイスクリームが直接溺死させているわけではない。
例:高級レストランが多い地域は平均寿命が長い
→高級レストランが多い地域は高所得者が多い。高所得者は医療へのアクセスが良い傾向にある。高級レストランが寿命をのばしているわけではない。
この場合、確率変数Zを除いたXとYの相関係数が真の相関係数と言える。
これを偏相関係数といい、以下のように計算される。
$$r_{XY \cdot Z} = \frac{r_{XY} – r_{XZ} r_{YZ}}{\sqrt{(1 – r_{XZ}^2)(1 – r_{YZ}^2)}}$$
様々な平均
平均にもいろいろある。
算術平均
$$\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n}$$
例:身長体重の平均
幾何平均
$$G = \sqrt[n]{x_1 \times x_2 \times \dots \times x_n}$$
例:各年の投資の年間成長率がわかっている時の平均成長率
調和平均
$$H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \dots + \frac{1}{x_n}}$$
例:速度の平均、単位時間あたりの作業効率
加重平均
$$\bar{x}_w = \frac{w_1 x_1 + w_2 x_2 + \dots + w_n x_n}{w_1 + w_2 + \dots + w_n}$$
例:経済指数、ポートフォリオの平均リターン
行列を用いた特性値
確率変数列\(X_n\)に対して、それぞれの平均\(\mu_i = E[X_i]\)で構成されるn次元ベクトル
$$\mu = (\mu_1, \mu_2, …\mu_n)^T$$
を平均ベクトルという。
また、\(X_i\)と\(X_j\)の共分散\(\sigma_{ij}\)の行列
$$\Sigma =
\begin{bmatrix}
\sigma_{11} & \sigma_{12} & \dots & \sigma_{1n} \\
\sigma_{21} & \sigma_{22} & \dots & \sigma_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
\sigma_{n1} & \sigma_{n2} & \dots & \sigma_{nn}
\end{bmatrix}$$
を分散共分散行列という。
さらに相関係数\(\rho_{ij}\)を要素とする行列
$$R =
\begin{bmatrix}
1 & \rho_{12} & \dots & \rho_{1n} \\
\rho_{21} & 1 & \dots & \rho_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
\rho_{n1} & \rho_{n2} & \dots & 1
\end{bmatrix}$$
を相関行列という。
まとめ
期待値:
$$E[X] = \int xf(x)dx $$
中央値:
$$P(x \leq a)=0.5$$
最頻値:
f(x)が最大となるx
一般的に右に裾が長い分布においては、最頻値<中央値<期待値
中央値は外れ値の値を受けにくい。
標準偏差:
$$\sigma = \sqrt{V[X]}$$
四分位範囲:
$$IQR = (P(x\leq{a})=0.75となるa) – (P(x\leq{b})=0.25となるb)$$
変動係数:
$$\sqrt{V[X]}/E[X]$$
裾が長い分布の時は四分位範囲、複数の確率変数を比べるときは変動係数。
共分散:
$$V[X+Y]=V[X]+V[Y]+2E{(X-\mu_1)(X-\mu_2)}$$
相関係数:
$$\rho_{xy} = \frac{Cov(X, Y)}{\sqrt{V[X]}\sqrt{V[Y]}}$$
偏相関係数:
$$r_{XY \cdot Z} = \frac{r_{XY} – r_{XZ} r_{YZ}}{\sqrt{(1 – r_{XZ}^2)(1 – r_{YZ}^2)}}$$
算術平均:
$$\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n}$$
幾何平均:
$$G = \sqrt[n]{x_1 \times x_2 \times \dots \times x_n}$$
調和平均:
$$H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \dots + \frac{1}{x_n}}$$
加重平均:
$$\bar{x}_w = \frac{w_1 x_1 + w_2 x_2 + \dots + w_n x_n}{w_1 + w_2 + \dots + w_n}$$
平均ベクトル:
$$\mu = (\mu_1, \mu_2, …\mu_n)^T$$
分散共分散行列:
$$\Sigma =
\begin{bmatrix}
\sigma_{11} & \sigma_{12} & \dots & \sigma_{1n} \\
\sigma_{21} & \sigma_{22} & \dots & \sigma_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
\sigma_{n1} & \sigma_{n2} & \dots & \sigma_{nn}
\end{bmatrix}$$
相関行列:
$$R =
\begin{bmatrix}
1 & \rho_{12} & \dots & \rho_{1n} \\
\rho_{21} & 1 & \dots & \rho_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
\rho_{n1} & \rho_{n2} & \dots & 1
\end{bmatrix}$$
今回は以上です!


コメント