フーリエ変換と波動方程式

フーリエ変換と波動方程式に関して勉強したのでまとめる。

元々フーリエ変換を勉強したかったのは、波動方程式を解きたかったからだ。

なぜ波動方程式を解きたかったかというと…特に理由はない。

なんか仕事に使えるかなって…(今のところ使えそうにはない)

フーリエ変換

まずフーリエ変換は以下のように定義される。

$$
\hat{u}(k, t) = \int_{-\infty}^\infty u(x, t) e^{-ikx} \, dx
$$

逆フーリエ変換は
$$
u(x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat{u}(k, t) e^{ikx} \, dk
$$

であり、\(u\)と\(\hat{u}\)が可積分であればフーリエの反転公式より、

$$
f(x) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat{f}(k) e^{ikx} \, dk
$$

波動方程式

弦の振動を表す方程式を考える。

位置x,時刻tにおける変位をu(x,t)とすると、

$$\frac{\partial^2 u(x, t)}{\partial t^2} = c^2 \frac{\partial^2 u(x, t)}{\partial x^2}$$

が成り立つ。これを一次元の波動方程式という。(c＞0は波の速度で定数)

今回はc=1、

初期条件\(u(x,0)=f(x), \frac{\partial u(x, 0)}{\partial t} = g(x)\)として解く

そのフーリエ変換は
$$
\frac{\partial^2 \hat{u}(k, t)}{\partial t^2} = -k^2 \hat{u}(k, t)
$$

となる。この常備分方程式を解くと、一般解は
$$
\hat{u}(k, t) = A(k) \cos(kt) + B(k) \sin(kt)
$$

となる。らしい(この一般解の求め方はよくわからなかったから飛ばした)。

さて、初期条件に対してもフーリエ変換すると、

まず、\(u(x, 0) = f(x)\)に関して、
$$
\hat{u}(k, 0) = \int_{-\infty}^\infty f(x) e^{-ikx} \, dx = \hat{f}(k)
$$
したがって、
$$
A(k) = \hat{f}(k)
$$

次に\(\frac{\partial u(x, 0)}{\partial t} = g(x) \)について考える。

$$\frac{\partial \hat{u}(k, 0)}{\partial t} = k B(k)$$
$$
\int_{-\infty}^\infty g(x) e^{-ikx} \, dx = \hat{g}(k)
$$
したがって、
$$
B(k) = \frac{\hat{g}(k)}{k}
$$

これらから常微分方程式の解は

$$
\hat{u}(k, t) = \hat{f}(k) \cos(kt) + \frac{\hat{g}(k)}{k} \sin(kt)
$$

となる。

次に、この関数を逆フーリエ変換してu(x,t)を求めれば良い。

つまり、

$$
u(x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \left[ \hat{f}(k) \cos(kt) + \frac{\hat{g}(k)}{k} \sin(kt) \right] e^{ikx} \, dk
$$

である。

さて、第1項を
$$
u_1(x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat{f}(k) \cos(kt) e^{ikx} \, dk
$$

第2項を
$$
u_2(x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \frac{\hat{g}(k)}{k} \sin(kt) e^{ikx} \, dk
$$

とする。

まず\(u_1(x, t)\)を考えると、

\(cos(kt)\) をオイラーの公式で書き換えて、
$$
\cos(kt) = \frac{e^{ikt} + e^{-ikt}}{2}
$$

これを代入すると
$$
u_1(x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat{f}(k) \frac{e^{i(k(x+t))} + e^{i(k(x-t))}}{2} \, dk
$$

この式を分離して
$$
u_1(x, t) = \frac{1}{4\pi} \int_{-\infty}^\infty \hat{f}(k) e^{i k (x+t)} \, dk + \frac{1}{4\pi} \int_{-\infty}^\infty \hat{f}(k) e^{i k (x-t)} \, dk
$$

さらにフーリエ反転公式を適用すると
$$
u_1(x, t) = \frac{1}{2} \left[ f(x+t) + f(x-t) \right]
$$

となる。

次に\(u_2(x, t)\)を考える。

\(sin(kt)\) をオイラーの公式で書き換えると、
$$
\sin(kt) = \frac{e^{ikt} – e^{-ikt}}{2i}
$$

これを代入して
$$
u_2(x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \frac{\hat{g}(k)}{k} \frac{e^{i(k(x+t))} – e^{i(k(x-t))}}{2i} \, dk$$

$$u_2(x, t) = \frac{1}{4\pi i} \int_{-\infty}^\infty \frac{\hat{g}(k)}{k} e^{i k (x+t)} \, dk – \frac{1}{4\pi i} \int_{-\infty}^\infty \frac{\hat{g}(k)}{k} e^{i k (x-t)} \, dk
$$

フーリエの性質により、次の関係が成り立つ
$$
\int_{-\infty}^\infty \frac{\hat{g}(k)}{k} e^{ikx} \, dk = \int_{-\infty}^x g(\xi) \, d\xi
$$

したがって、
$$
u_2(x, t) = \frac{1}{2} \int_{x-t}^{x+t} g(\xi) \, d\xi
$$

さて、弦が静止した状態から叩くことを想定すると、初期速度はg(x)=0で、

これを図示すると以下のようになり、波の挙動を示していることがわかる。

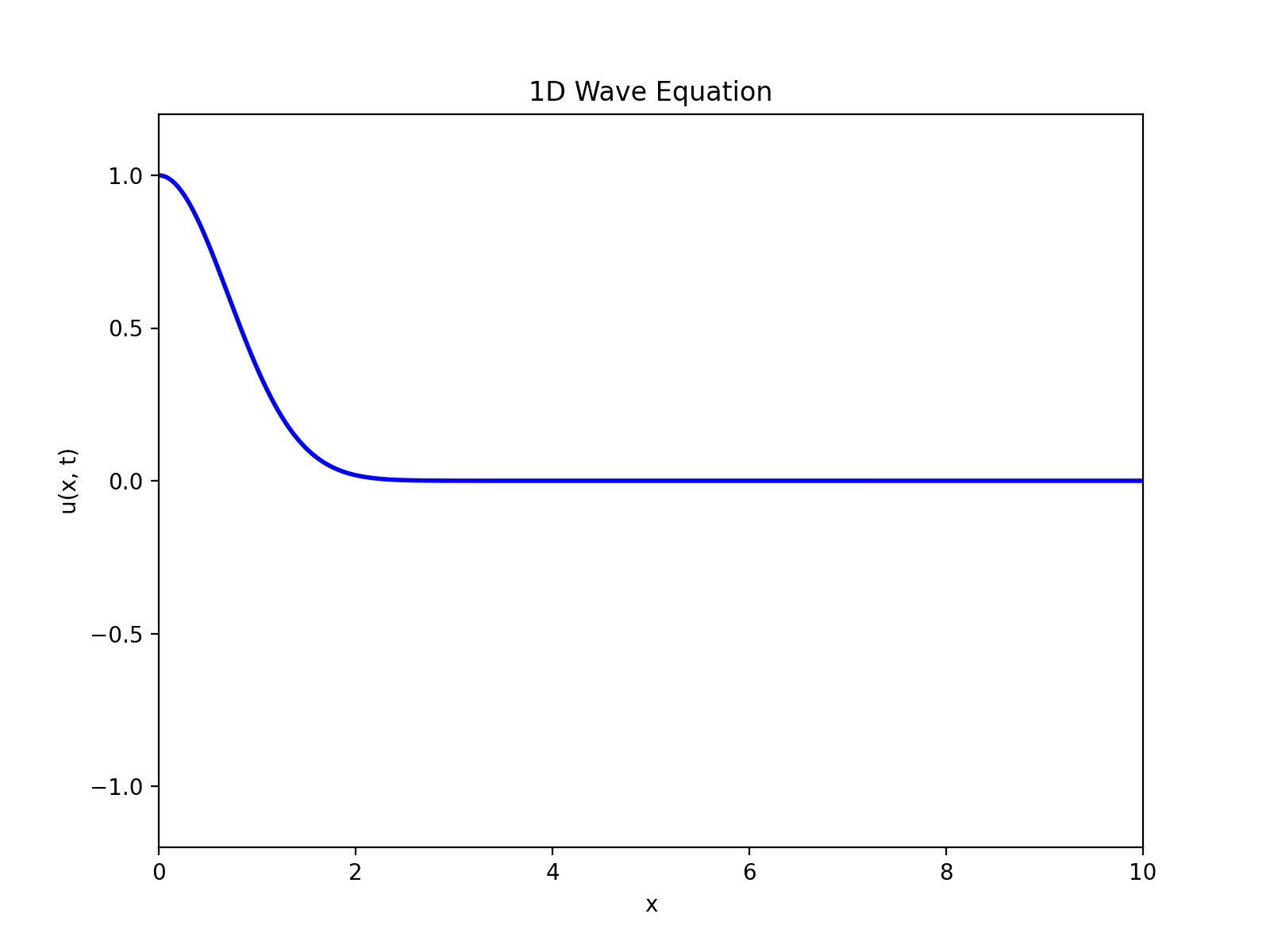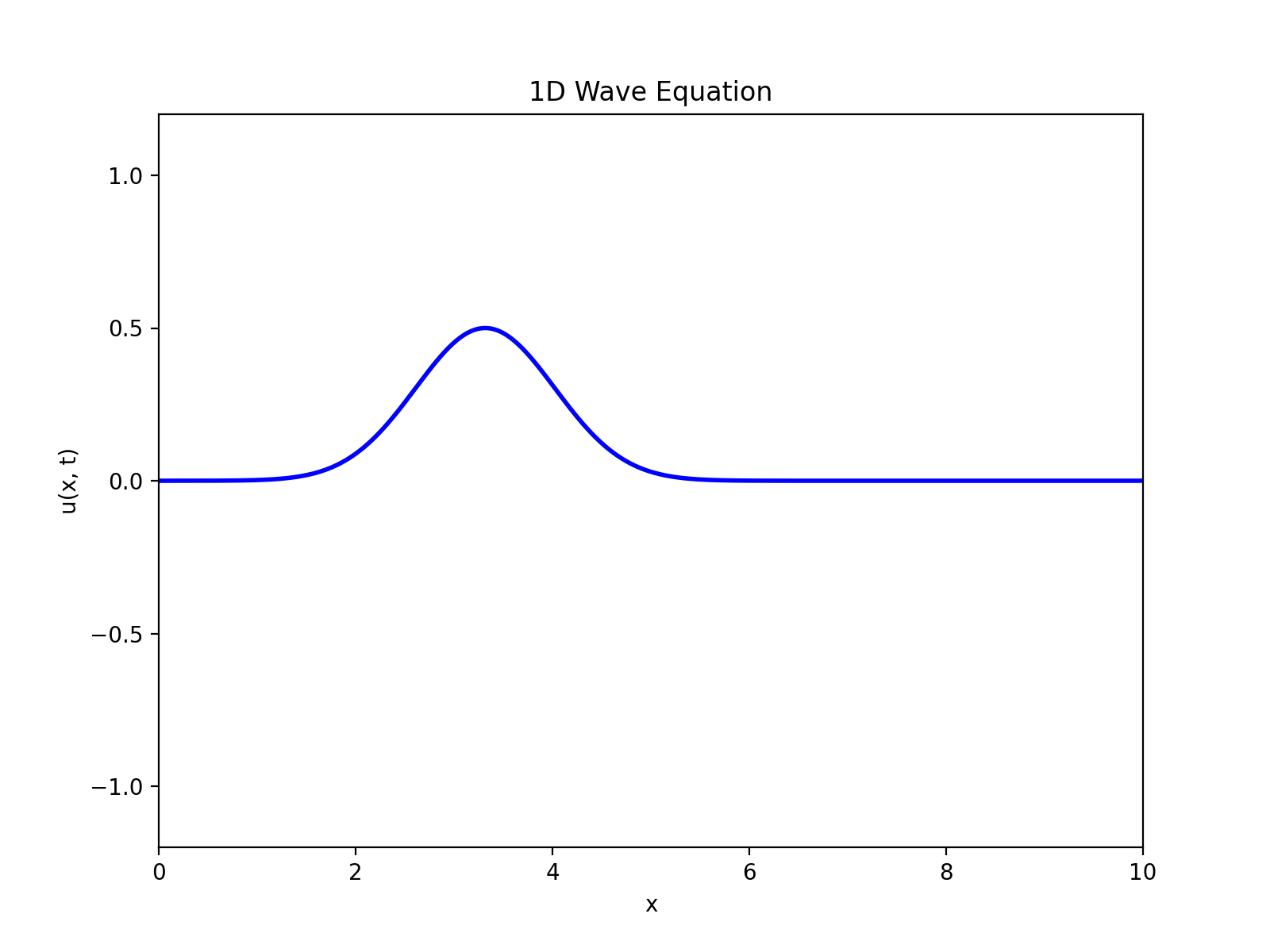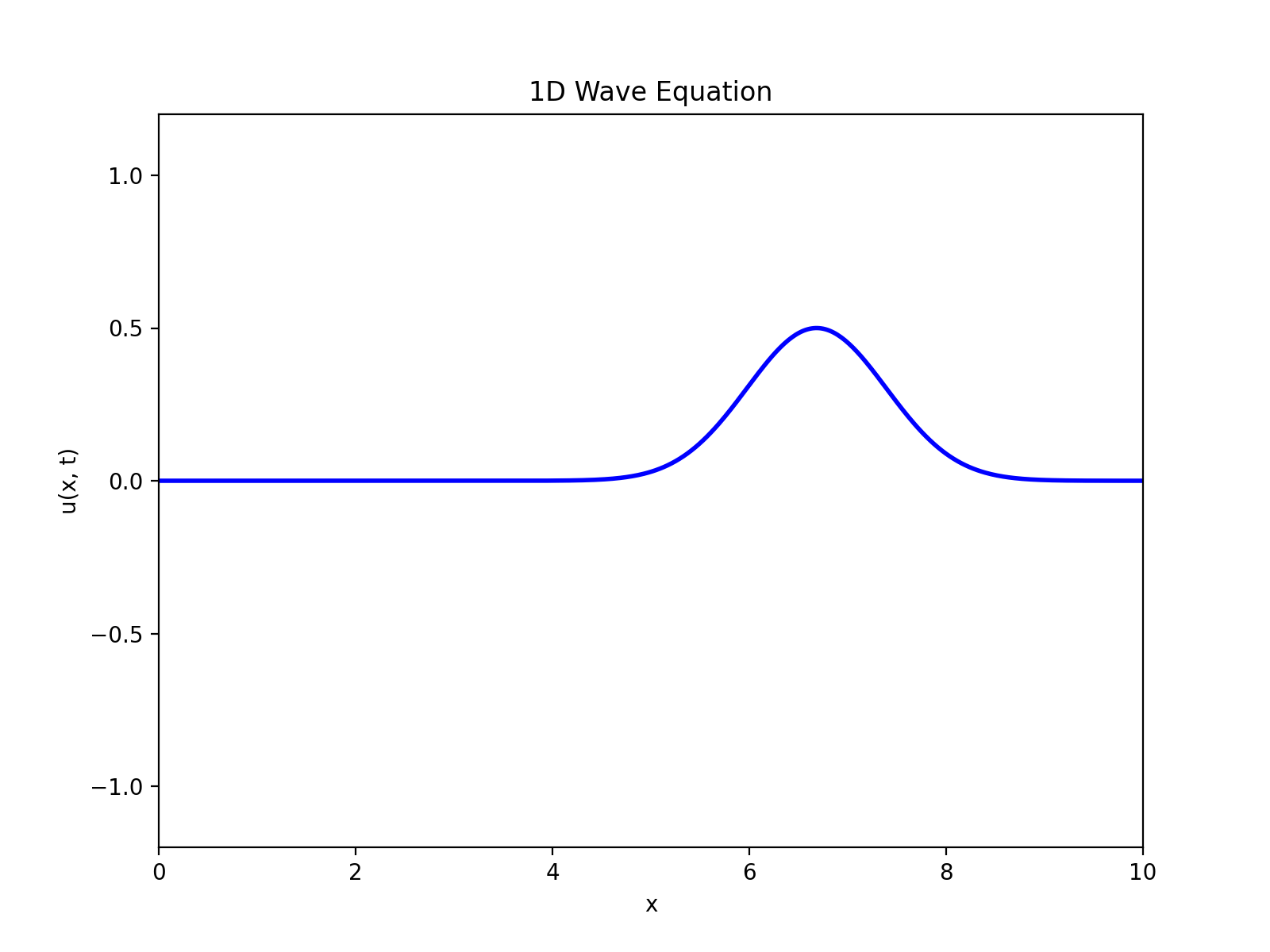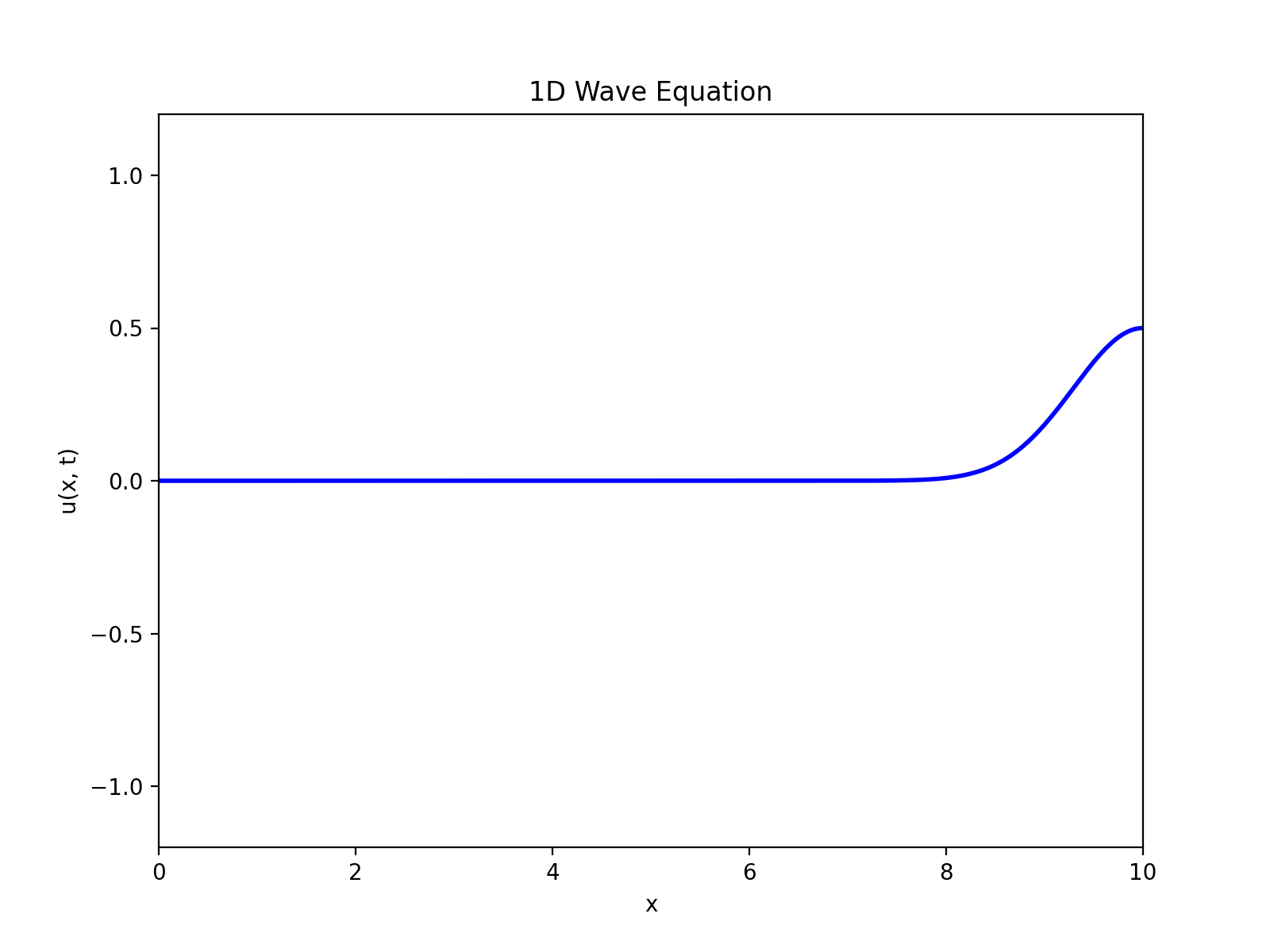
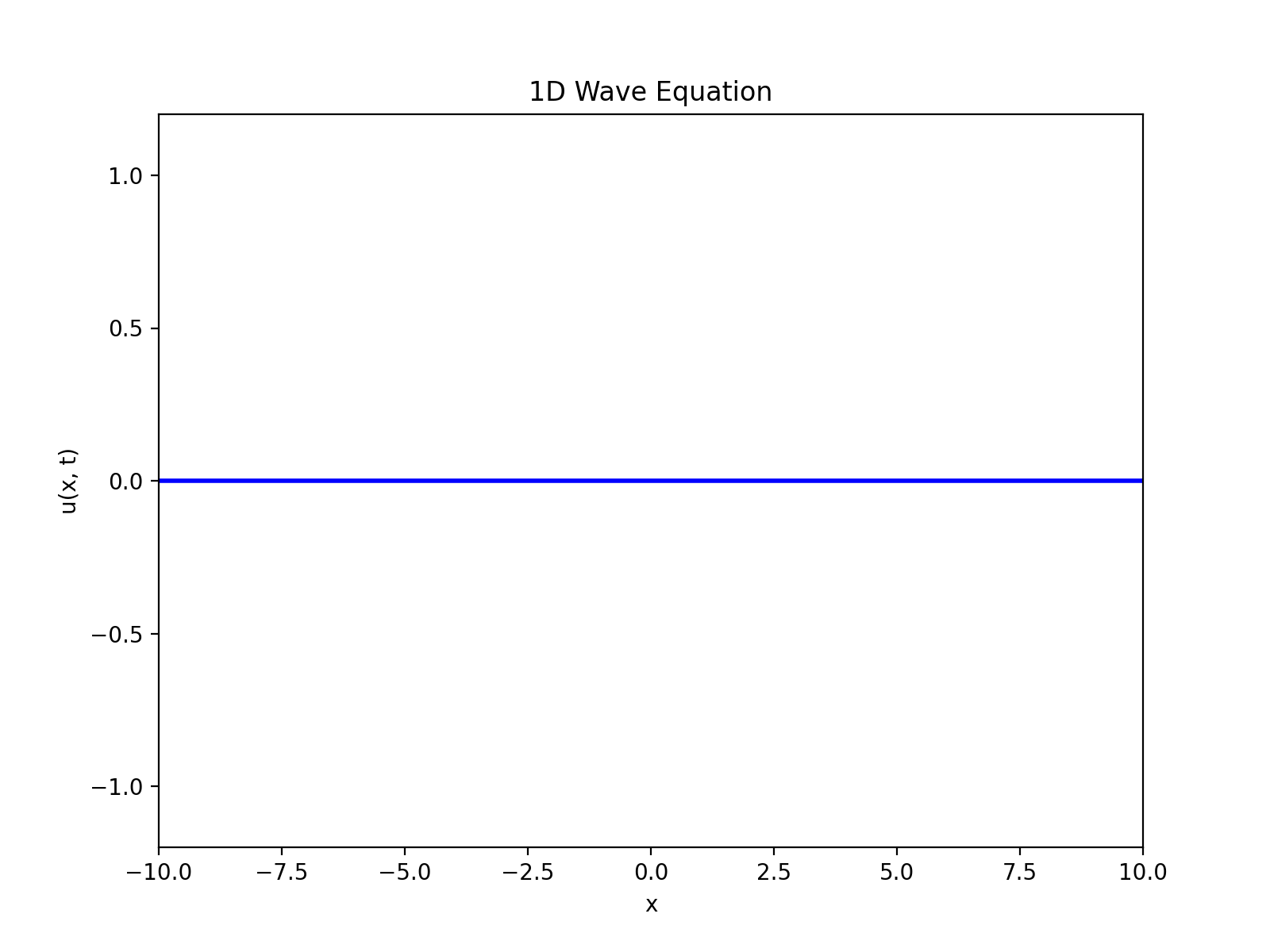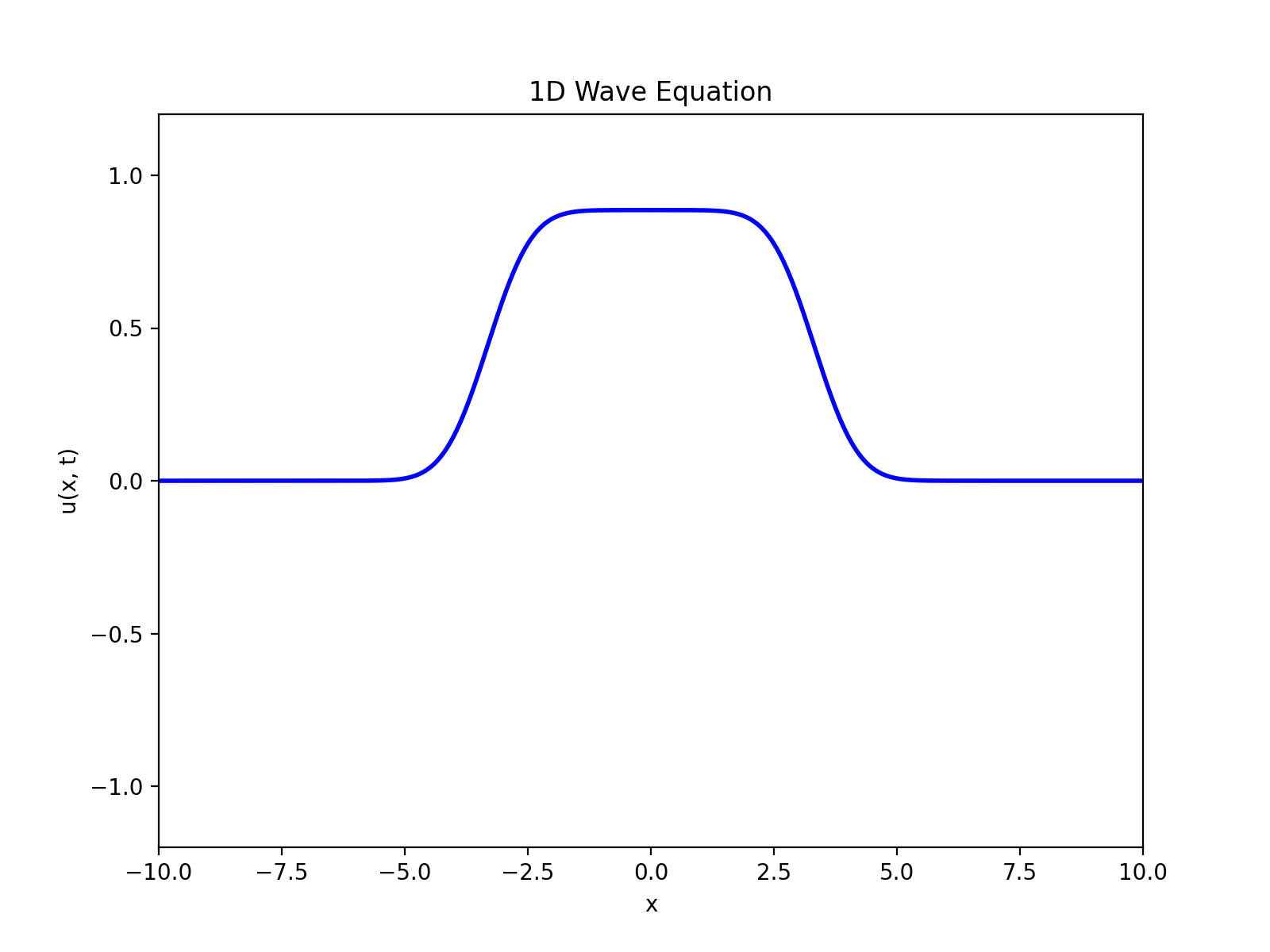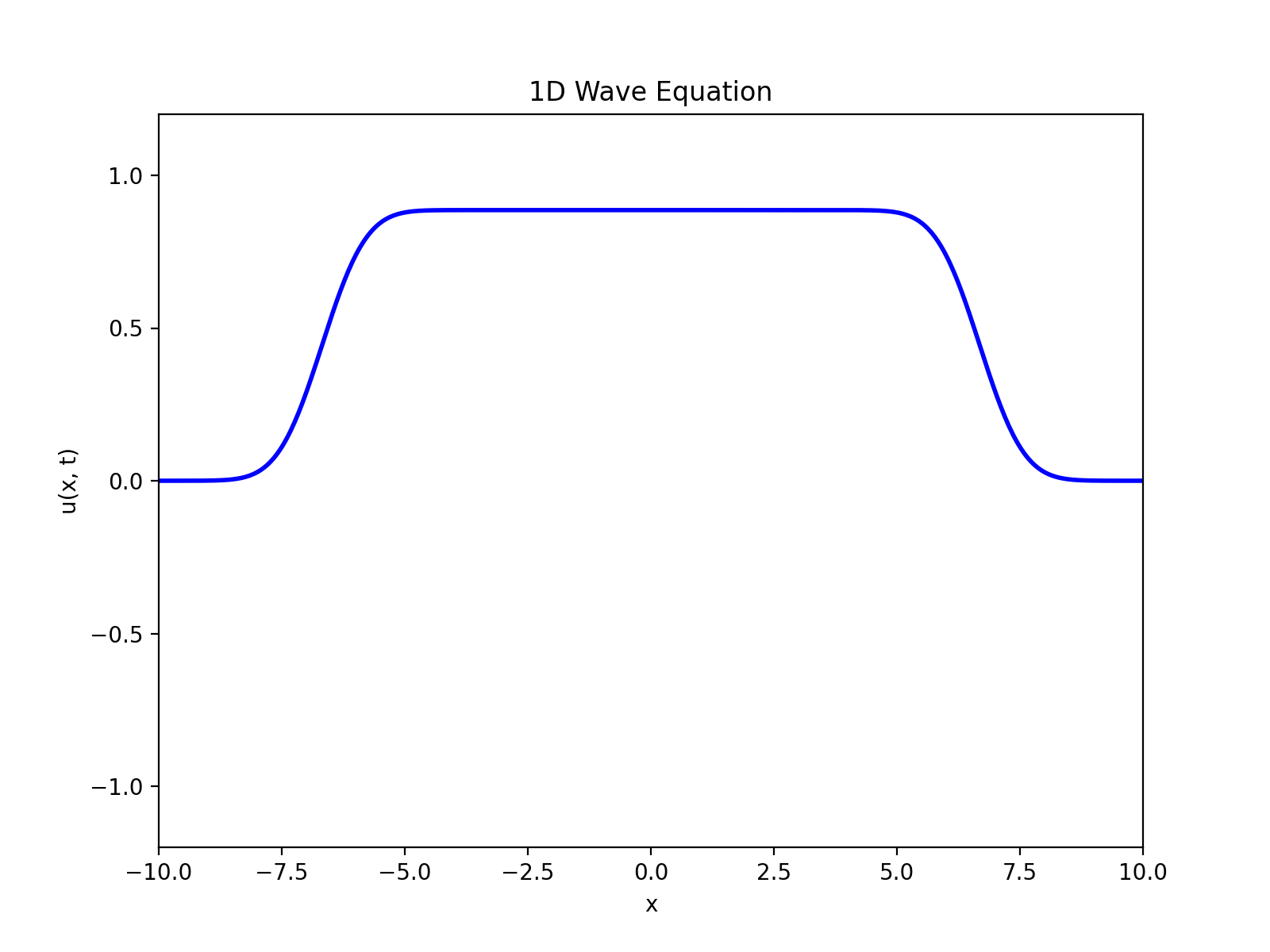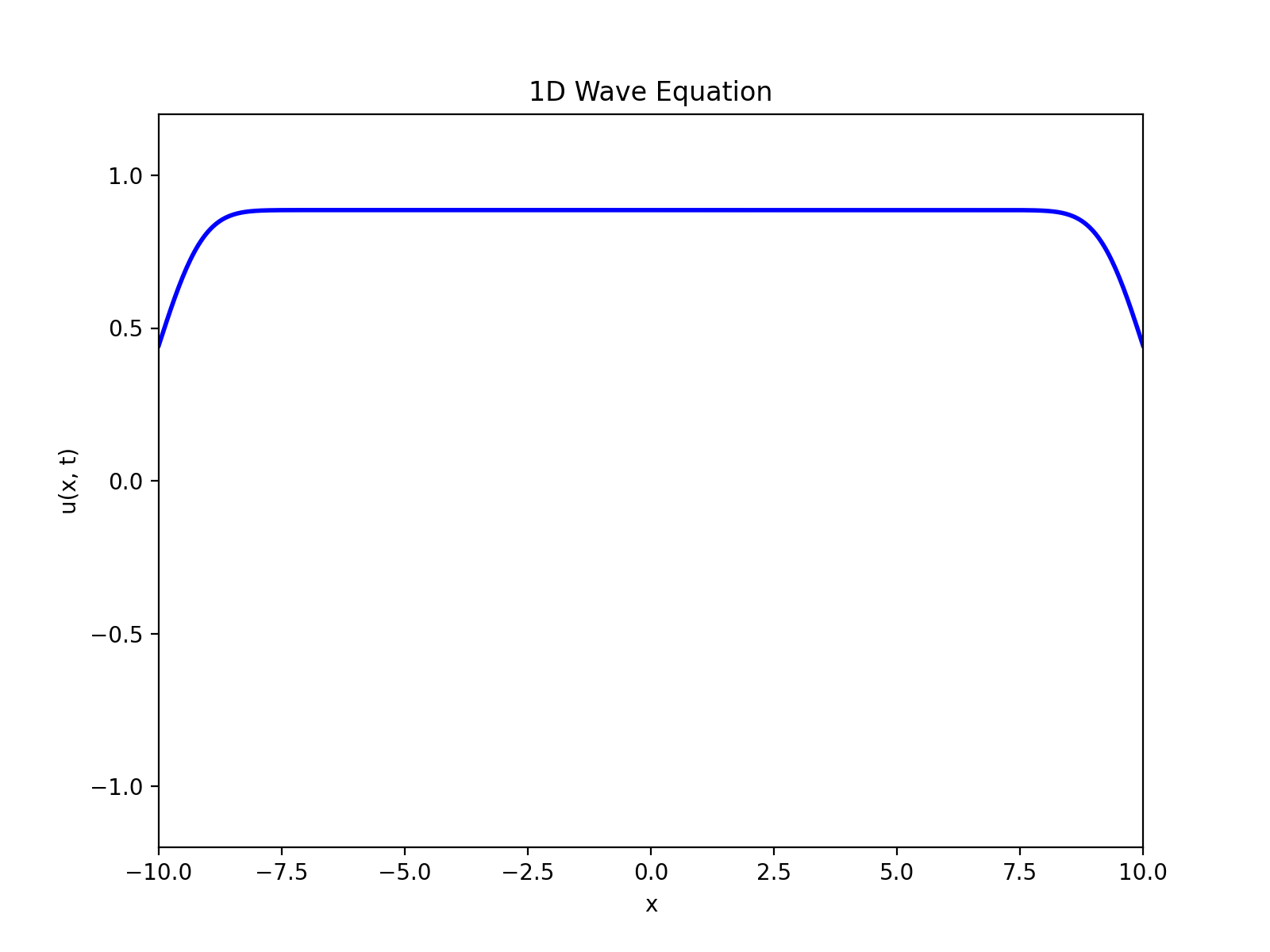
次に初期変位なし、初期速度ありの状況を考える。

今回紹介した波動方程式だと、外力は時間依存しないので、最終的にu(x,t)が一定になってしまった。

実際の波動方程式の場合はF(x,t)という項を付け加えることで、時間依存性を考慮した速度分布が計算できる(らしい)。

感想

今回はそんなところです。

あとは流体力学、統計力学、位相幾何学を勉強すれば‥ふふふ。

とか考えてたけどその前に寿命が来そう。

ていうかまずは統計学やろう。あーでも経済学とかビジネス方面の勉強もしたいし、、英語も、、

ていうかプログラミングも最近疎かだし、、、

やりたいことが多すぎて困ってます。

コードの覚え書きも載せておく。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter

# 波動のパラメータ
c = 1.0  # 波動の速度
x = np.linspace(-10, 10, 500)  # xの範囲
t_values = np.linspace(0, 10, 200)  # 時間の範囲

# 初期条件関数
def initial_displacement(x):
    return 0  # 初期変位

def initial_velocity(x):
    return np.exp(-x ** 2)  # 初期速度

# 波動方程式の解
def wave_solution(x, t, c):
    #ダランベールの公式の第一項
    term_1 = 0.5 * (initial_displacement(x - c * t) + initial_displacement(x + c * t))

    #第2項
    integral_term = np.zeros_like(x)
    for i, xi in enumerate(x):
        lower_limit = xi - c * t
        upper_limit = xi + c * t
        # 数値積分 (初期速度関数をトラペゾイド則で積分)
        integration_points = np.linspace(lower_limit, upper_limit, 100)
        integral_term[i] = np.trapz(initial_velocity(integration_points), integration_points)

    term_2 = (1 / (2 * c)) * integral_term

    return term_1 + term_2


# グラフ描画用の準備
fig, ax = plt.subplots(figsize=(8, 6))
line, = ax.plot([], [], lw=2, color='blue')
ax.set_xlim(-10, 10)
ax.set_ylim(-1.2, 1.2)
ax.set_title("1D Wave Equation")
ax.set_xlabel("x")
ax.set_ylabel("u(x, t)")

# アニメーション更新関数
def update(frame):
    t = t_values[frame]
    y = wave_solution(x, t, c)
    line.set_data(x, y)
    return line,

# アニメーションの生成
ani = FuncAnimation(fig, update, frames=len(t_values), interval=50, blit=True)
plt.show()


# アニメーションを保存する
filename = "wave_equation.gif"  # 保存ファイル名
writer = PillowWriter(fps=20)  # GIF用のライター
ani.save(filename, writer=writer)
print(f"Animation saved as {filename}")