確率収束
任意の正の定数\(\epsilon\)について、確率分布の平均を\(\mu\)、その分布からn個サンプルを取り出した時の標本平均を\(\bar{X_n}\)とする。
このとき、
$$P\big(|\overline{X}_n – \mu| < \varepsilon\big) \to 1 \quad (n \to \infty)$$
となることを\(\bar{X_n}\)は\(\mu\)に確率収束するという。
これがいわゆる「大数の法則」である。
下記はコインを投げまくった時に表が出る確率が収束していく様である。
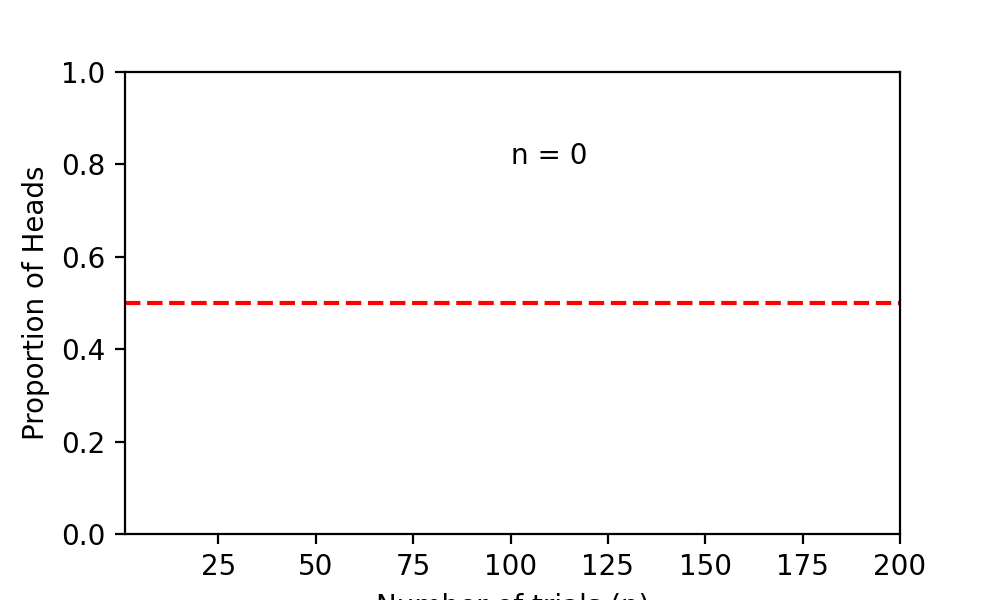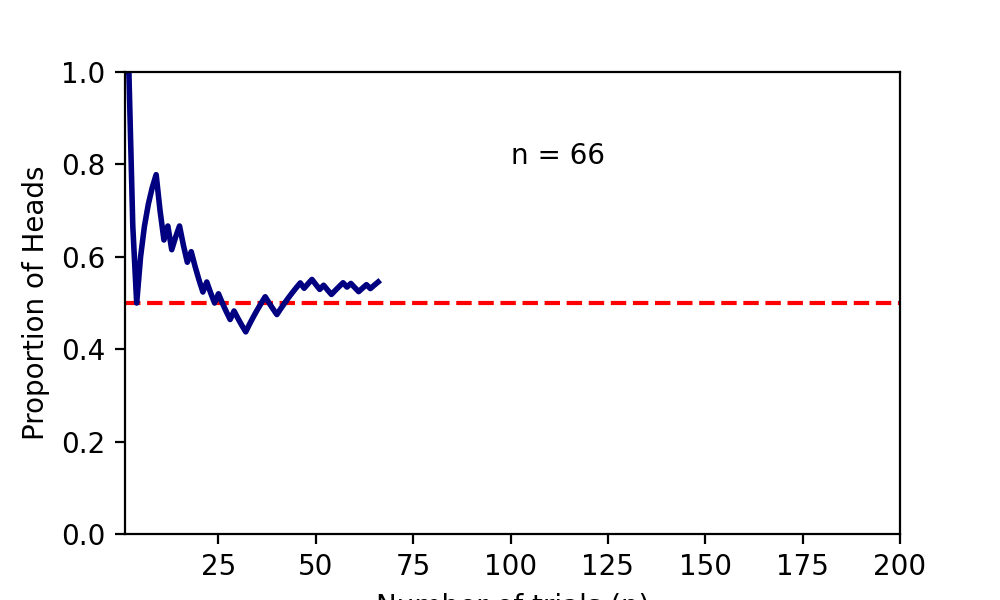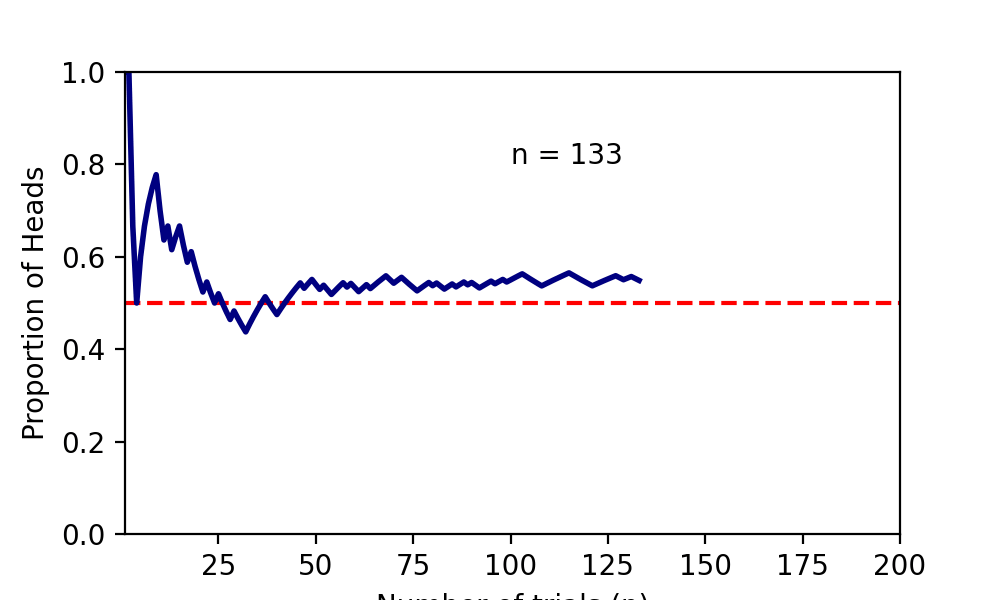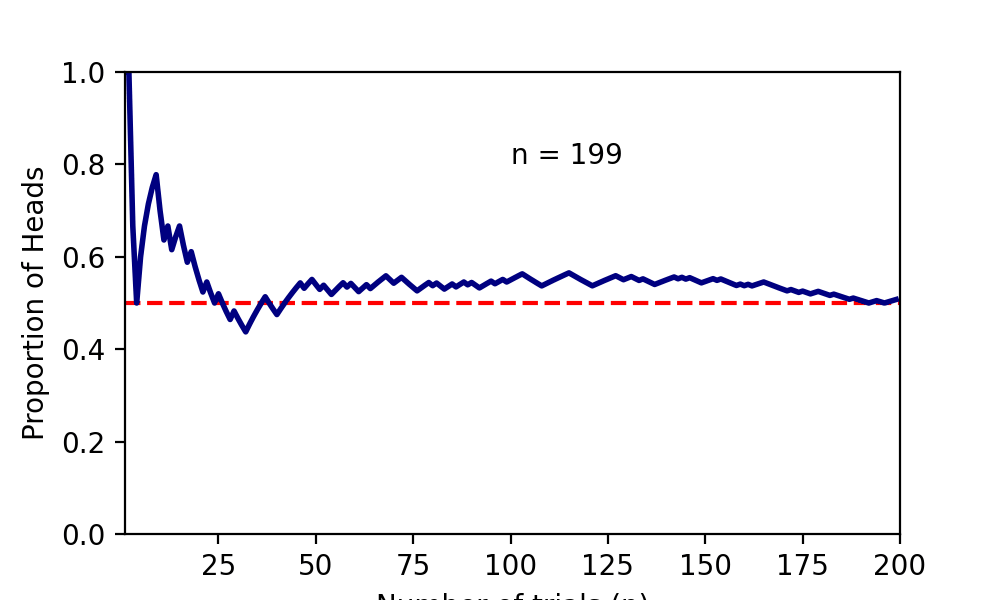
確率分布の収束
先ほどは「確率」収束を考えたが、次に「確率分布」の収束を考える。
確率変数列 \( X_n \) の分布関数を
\( F_n(x) = P(X_n < x) \)
としたとき、\( X_n \) がある確率分布 \( G \) に**分布収束(distribution convergence)**するとは、
\(lim_{n \to \infty} F_n(x) = G(x)\)
が、すべての連続点 \( x \) で成り立つということである。
例:\( X_n \sim N(0, \frac{1}{n}) \) はどのような確率変数に収束するかを考える。
各 \( X_n \) の分布関数は
$$F_n(x) = P(X_n \le x) = \Phi(\sqrt{n}x)$$
である。ただし \( \Phi \) は標準正規分布の分布関数。
ここで \( n \to \infty \) の極限をとると、
\( \sqrt{n}x \) の符号によって値が変わる:
$$\lim_{n \to \infty} F_n(x) =$$
\begin{cases}
0 & (x < 0) \\
\frac{1}{2} & (x = 0) \\
1 & (x > 0)
\end{cases}$$
この極限関数 \( G(x) \) は、確率がすべて 0 に集中するディラック分布 \( \delta_0 \) の分布関数に一致する。
すなわち、\( X_n \) は「確率1で0をとる定数確率変数」に分布収束する。
※x=0では一致しないのだが、連続点ではないのでセーフなのである。
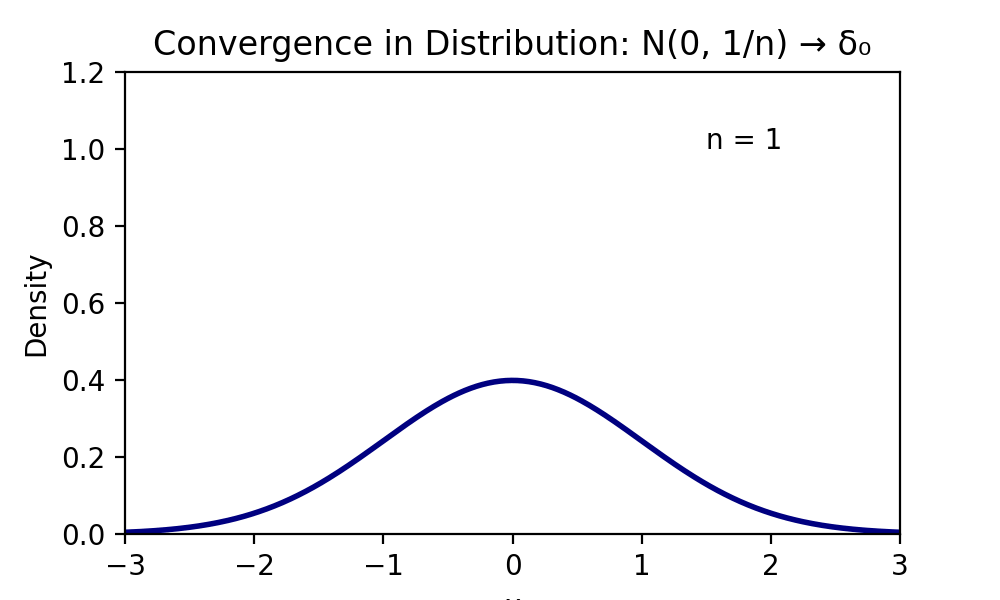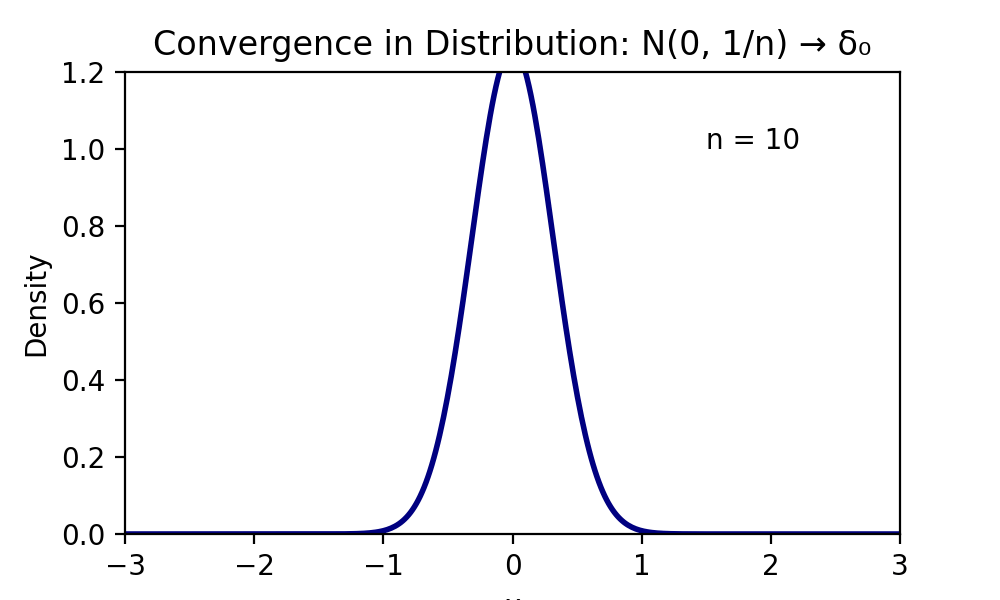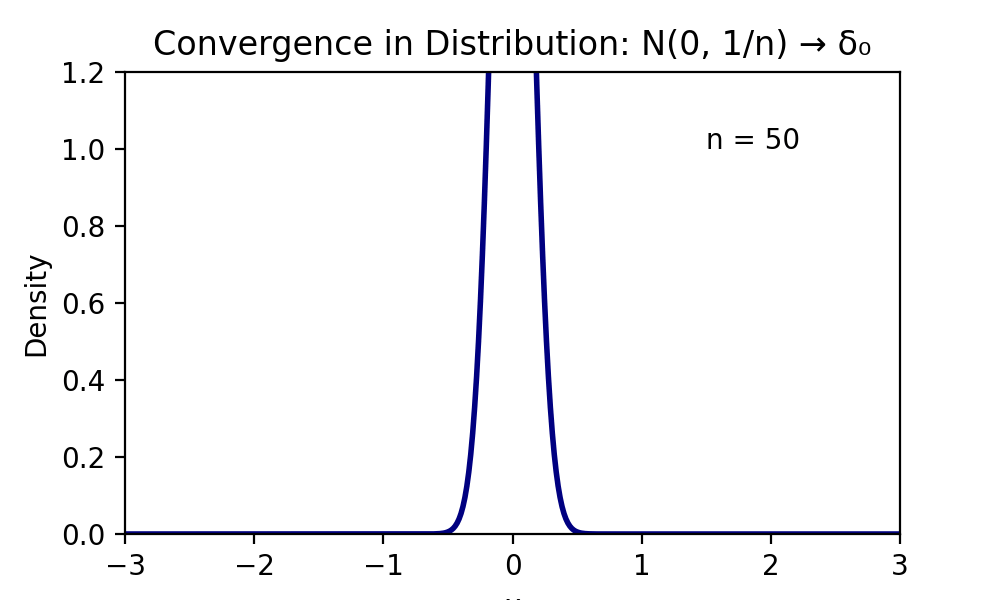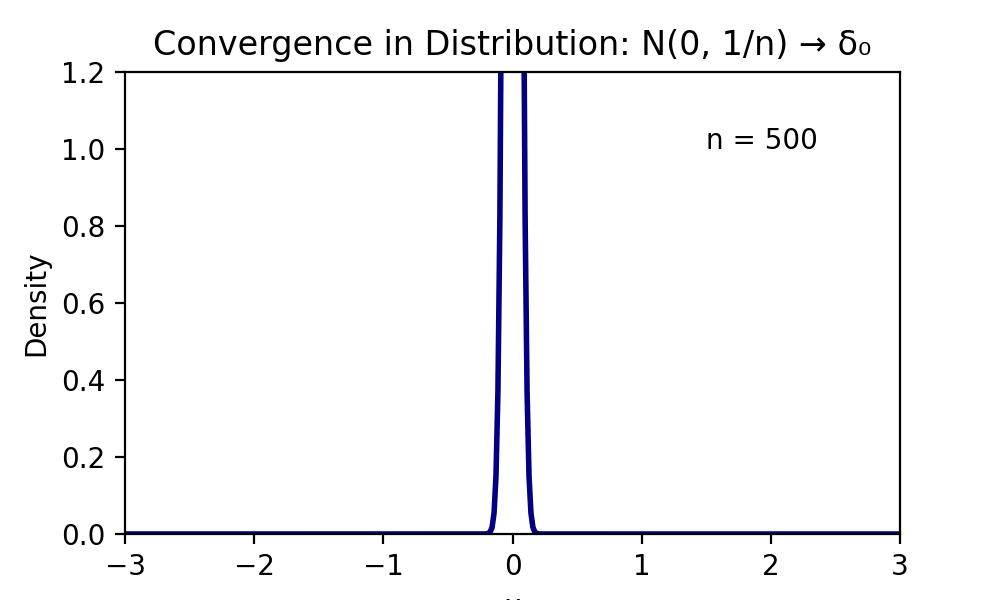
分布収束の法則
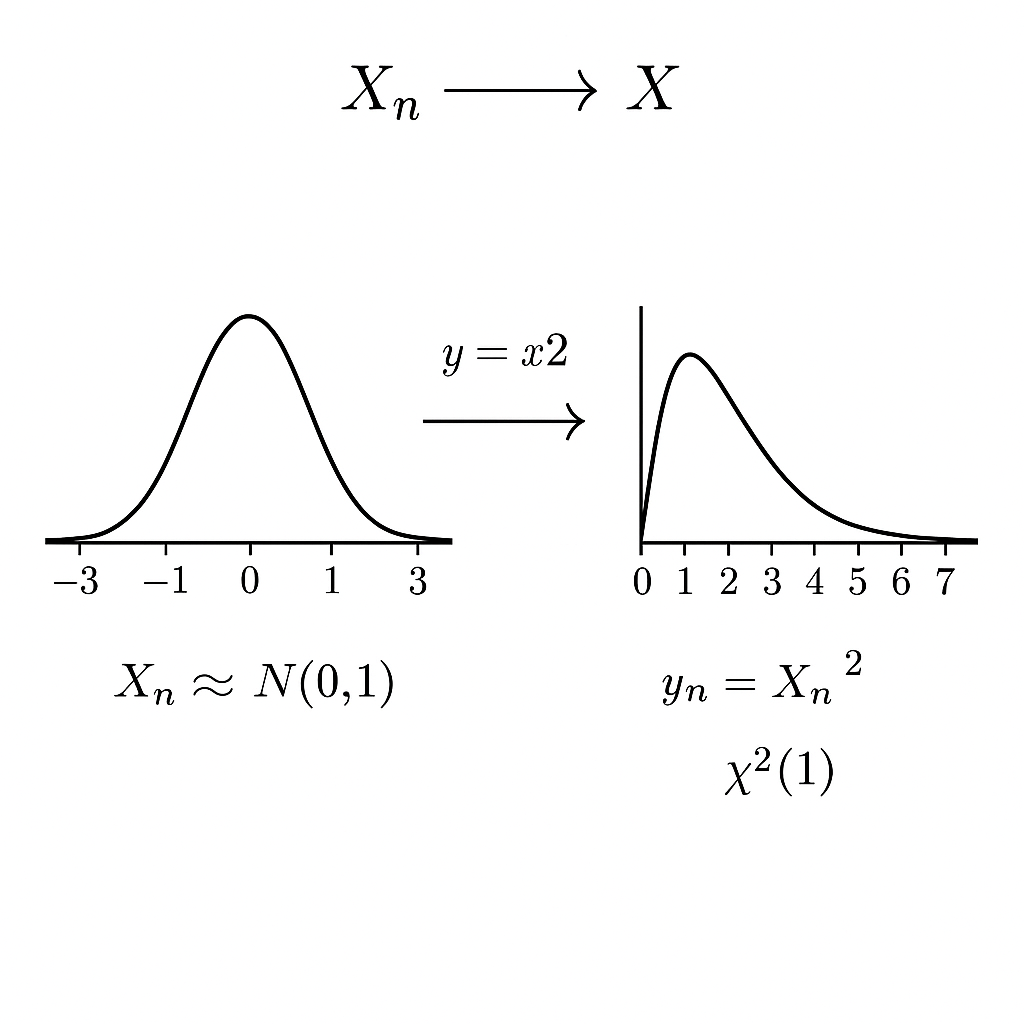
連続写像定理
確率変数列 \(X_n\) が分布収束して \(X_n \to X\)
となっており、関数
\(g: \mathbb{R} \to \mathbb{R} \)が 連続 であるとする。
すると
$$g(X_n) \to g(X)$$
が成り立つ。
スルツキーの補題
確率変数列 \(X_n、Y_n\) について、
$$X_n \to_d X, \qquad Y_n \to_p c$$
(c は定数)
が成り立つとき、次が成立する。
● 和
$$X_n + Y_n \to_d X + c$$
● 積
$$X_n Y_n \to_d Xc$$
デルタ法
\({X_n}\)が平均\(\mu\)、分散\(\sigma\)の独立分布に従うとする。
また\({X_n}\)の標本平均を\(\bar{X_n}\)とする。
このとき、連続かつ微分可能な関数f(x)を用いて、
\(\sqrt{n}(f(\bar{X_n})-f(\mu))\)の分布収束先を考える。
テイラーの定理より、
$$f(\bar{X_n}) = f(\mu)+f'(\mu)(\bar{X}_n – \mu)+o(\bar{X}_n – \mu)$$
となる。ここで \(o(\bar{X}_n – \mu)\) は、\(\bar{X}_n \to \mu\) のときに
\((\bar{X}_n – \mu)\) よりも速く 0 に近づく項である。
上式を \(\sqrt{n}\) 倍すると、
$$\sqrt{n}f(\bar{X_n}) = \sqrt{n}f(\mu)+f'(\mu)\sqrt{n}(\bar{X}_n – \mu) + \sqrt{n}o(\bar{X}_n – \mu)$$
というわけで、
$$\sqrt{n}(f(\bar{X_n}) – f(\mu)) \approx f'(\mu)\sqrt{n}(\bar{X}_n – \mu)$$
中心極限定理より、
\(\sqrt{n}(\bar{X}_n – \mu)\)は\(N(0, \sigma^2)\)に従うので、
\(\sqrt{n}(f(\bar{X_n})-f(\mu))\)は\(N(0, f'(\mu)^2\sigma^2)\)に従う。
これをデルタ法という。


コメント