正規分布(ガウス分布)
確率密度関数
$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x – \mu)^2}{2\sigma^2}\right)$$
を満たす分布を正規分布という。
その期待値と分散は\(\mu\)と\(\sigma^2\)となる。
正規分布の特徴として、
- Xが正規分布N(\(\mu\), \(\sigma^2\))に従うとき、線形変換Y=aX+bはN(\(a\mu+b\), \(a^2\sigma^2\))に従う。
- 標準化変数\(Z=\frac{X-\mu}{\sigma}\)は標準正規分布N(0,1)に従う。
このことから、正規分布の確率計算は標準正規分布に帰着できる。
ここで、標準正規分布の累積分布関数は
$$\Phi(z) = P(X \leq z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}} dt$$
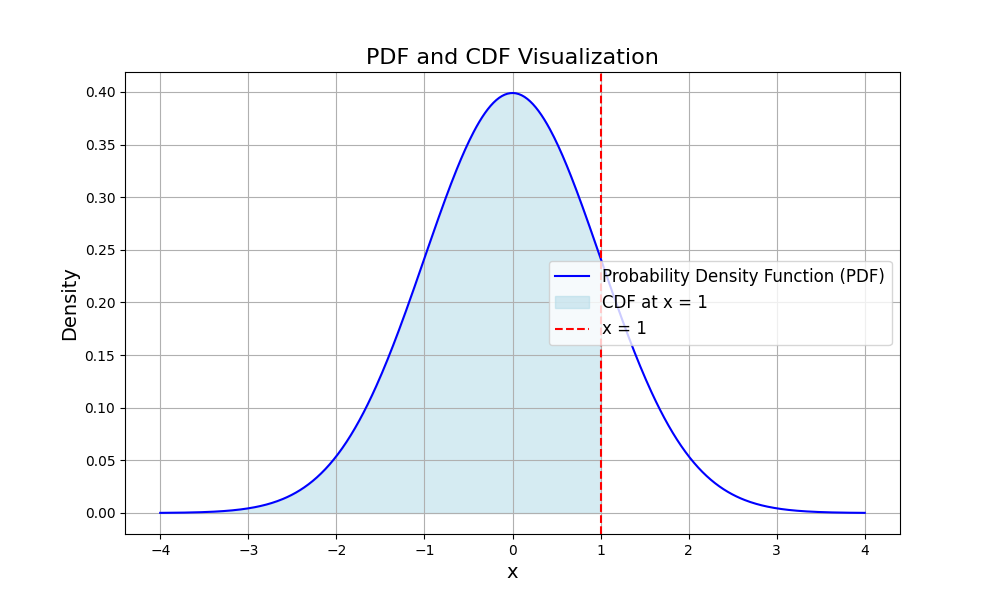
これがよく見る正規分布表のやつですね。
指数分布
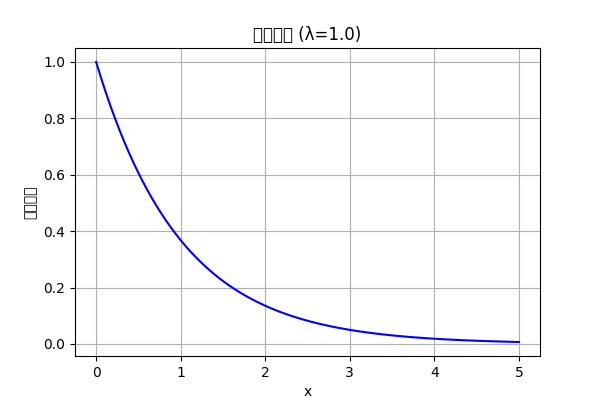
文字化けしてるけど指数分布。
あるイベント(故障、死亡など)が生じるまでの時間を示す。
システムの故障までの時間や、寿命などの分布に用いられる。
確率関数(累積分布関数, CDF):
$$ F(x) = P(X \leq x) = \begin{cases} 1 – e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases} $$
確率密度関数(PDF):
$$ f(x) = \begin{cases} \lambda e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases} $$
期待値:
$$ E[X] = \frac{1}{\lambda} $$
分散:
$$ \text{Var}(X) = \frac{1}{\lambda^2} $$
ガンマ分布
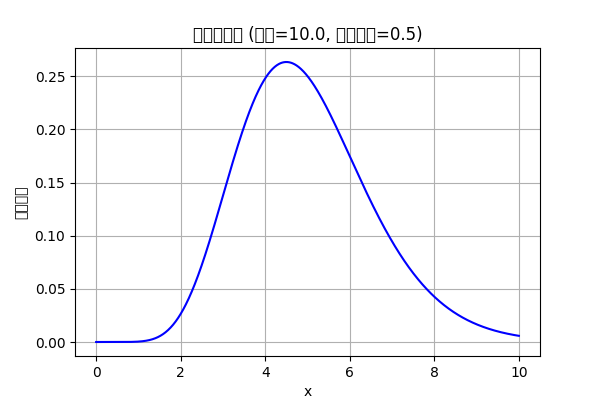
指数分布をより一般化することを考える。
すなわち、あるイベントがα回生じるまでにかかる時間を考える。
この時、確率関数は、
$$
f(x) = \frac{\lambda^\alpha x^{\alpha – 1} e^{-\lambda x}}{\Gamma(\alpha)}, \quad (x \geq 0)
$$
なお、
$$
\Gamma(\alpha) = \int_0^{\infty} t^{\alpha – 1} e^{-t} dt
$$
で、これをガンマ関数という。
期待値と分散はそれぞれ
$$
E[X] = \frac{\alpha}{\lambda}
$$
$$
\text{Var}(X) = \frac{\alpha}{\lambda^2}
$$
となる。
前述の通りガンマ分布は指数分布を拡張したものだから、α=1の場合は指数分布に一致する。
ベータ分布
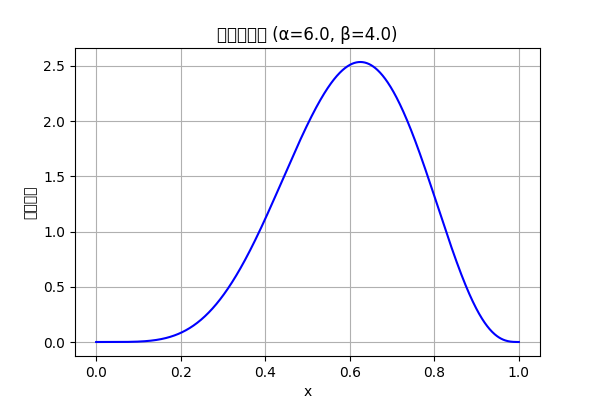
(0,1)上確率の確率変数が以下の確率密度関数
$$
f(x) = \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{B(\alpha, \beta)}, \quad 0 \leq x \leq 1
$$
を満たすとき、これをベータ分布という。
αとβはそれぞれ成功、失敗に影響するパラメータ
なお、
$$
B(\alpha, \beta) = \int_0^1 t^{\alpha – 1} (1 – t)^{\beta – 1} dt
$$
で、これをベータ関数という。
ベータ関数はガンマ関数で表すことができて、
$$
B(\alpha, \beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)}
$$
である。またベータ分布の期待値と分散は
$$
E[X] = \frac{\alpha}{\alpha + \beta}
$$
$$
\text{Var}(X) = \frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}
$$
となる。
多次元正規分布
独立ではない多数の正規分布を仮定して用いられる確率分布を多次元正規分布という。
まず、簡略のために二次元正規分布を考える。
標準正規分布N(0.1)に従う独立な確率変数X1とX2がある時、変換
$$Y_1 = aX_1+bX_2, Y_2 = cX_1+dX_2$$
を定義する。
この時、Y1とY2の期待値μ1とμ2は
$$\mu_1 = E[Y_1]=E[aX_1+bX_2] = aE[X_1]+bE[X_2]$$
ここで\(E[X_1]=E[X_2]=0\)だから、μ2についても同様に考えて、
$$\mu_1 = \mu_2 = 0$$である。
次に分散についても同様にσ1, σ2として考えると、
$$\sigma_1^2 = V[aX_1+bX_2] = a^2+b^2$$
同様に
$$\sigma_2^2 = c^2+d^2$$
またX1とX2は独立だが、Y1とY2は独立ではないため、その共分散σ12は
$$\sigma_{12} = E[Y_1Y_2]-E[Y_1]E[Y_2] = E[Y_1Y_2]$$
$$E[Y_1Y_2] = E[(aX_1+bX_2)(cX_1+dX_2)] = E[acX_1^2+cdX_2^2]=ac+bd$$
これで、各分散と共分散がわかったので、相関係数を計算してみる。
$$\rho = \frac{ac+bd}{\sqrt{(a^2+b^2)(c^2+d^2)}}$$
さて、いま考えたいのは独立でないY1とY2の同時確率密度関数だが、
まずは簡単なX1、X2の同時確率密度関数を考える。
X1とX2は独立にN(0,1)に従うことから同時確率密度関数はそれらの積で表され、
$$
f(x_1, x_2) = f_{X_1}(x_1) f_{X_2}(x_2) = \left( \frac{1}{\sqrt{2\pi}} e^{-\frac{x_1^2}{2}} \right) \left( \frac{1}{\sqrt{2\pi}} e^{-\frac{x_2^2}{2}} \right) …①
$$
$$
= \frac{1}{2\pi} e^{-\frac{x_1^2 + x_2^2}{2}}, \quad -\infty < x_1, x_2 < \infty
$$
となる。
Y1,Y2について考える場合は最初に定義した変換の逆変換
$$\begin{bmatrix} X_1 \\ X_2 \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1}\
\begin{bmatrix} Y_1 \\ Y_2 \end{bmatrix}$$
を考える。
ここで出てくる逆行列は
$$A^{-1} = \frac{1}{ad – bc}\
\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$$
であり、
$$\begin{bmatrix} X_1 \\X_2 \end{bmatrix}=\frac{1}{ad – bc}
\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
\begin{bmatrix} Y_1 \\ Y_2 \end{bmatrix}$$
である。よってX1、X2は以下のようにかける。
$$X_1 = \frac{dY_1 – bY_2}{ad – bc}, \quad X_2 = \frac{-cY_1 + aY_2}{ad – bc}$$
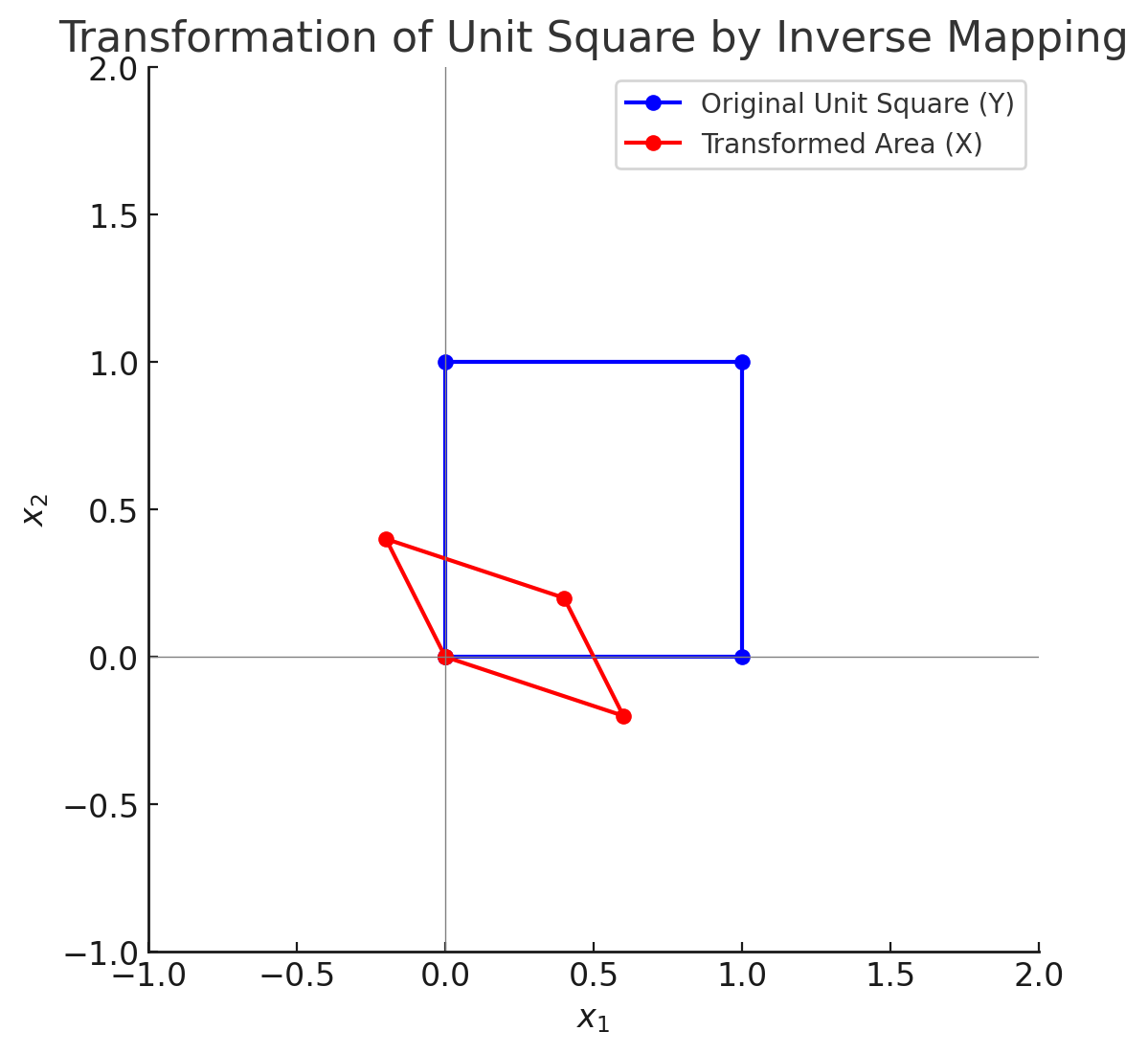
確率密度関数は面積あたりの関数であるから、逆変換に伴う面積の伸縮率を考慮する。
そのため(y1,y2)=(0,0), (0,1), (1,0), (1,1)とした単位正方形が逆変換によってどう伸縮するかを調べる。
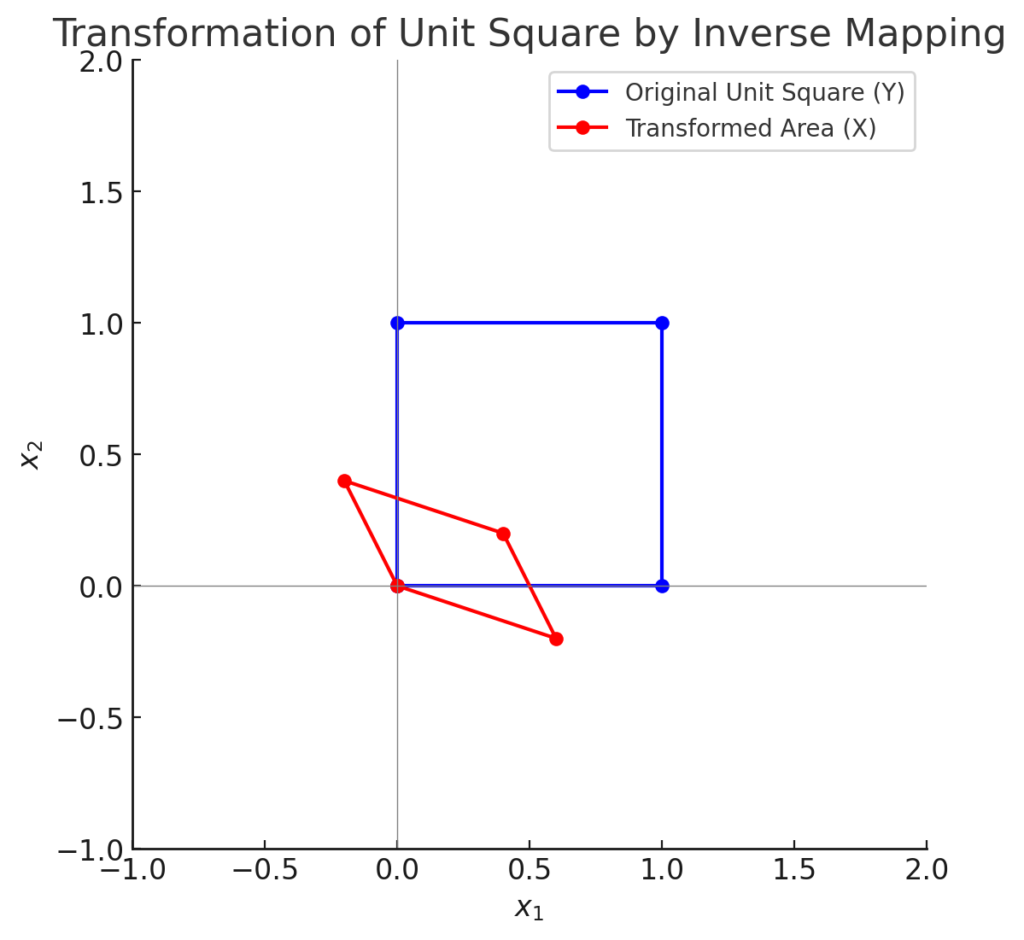
これは、2変数の変数変換で行ったヤコビアンと同じこと(ヤコビアンが面積の変化率)で、
$$J =\begin{bmatrix}
\frac{\partial X_1}{\partial Y_1} & \frac{\partial X_1}{\partial Y_2} \\
\frac{\partial X_2}{\partial Y_1} & \frac{\partial X_2}{\partial Y_2}\end{bmatrix}=\begin{bmatrix}
\frac{d}{ad – bc} & \frac{-b}{ad – bc} \\
\frac{-c}{ad – bc} & \frac{a}{ad – bc}
\end{bmatrix}$$
$$J =
\begin{bmatrix}
\frac{\partial Y_1}{\partial X_1} & \frac{\partial Y_1}{\partial X_2} \\
\frac{\partial Y_2}{\partial X_1} & \frac{\partial Y_2}{\partial X_2}\end{bmatrix}=\begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix} \cdot \frac{1}{ad – bc}$$
$$
\left| \det J \right| = \left| \frac{1}{ad – bc} \right|
$$
よってY1とY2の同時確率密度関数は以下のように表せる。
$$
f_{Y_1, Y_2}(y_1, y_2) = f_{X_1, X_2}(x_1, x_2) \cdot \left| \det J \right|
$$
これを計算して、
$$f_{Y_1, Y_2}(y_1, y_2) = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1 – \rho^2}}
\exp \left( -\frac{1}{2(1 – \rho^2)}
\left[ \frac{(y_1 – \mu_1)^2}{\sigma_1^2}-\frac{2\rho (y_1 – \mu_1)(y_2 – \mu_2)}{\sigma_1 \sigma_2}+\frac{(y_2 – \mu_2)^2}{\sigma_2^2} \right] \right)$$
となる。
さて、これをベクトルで表現すると、
$$\mathbf{Y} =
\begin{bmatrix}
Y_1 \\
Y_2
\end{bmatrix}$$
となり、平均ベクトルと分散共分散行列は、
$$\boldsymbol{\mu} =
\begin{bmatrix}
\mu_1 \\
\mu_2
\end{bmatrix}, \quad
\Sigma =
\begin{bmatrix}
\sigma_1^2 & \rho \sigma_1 \sigma_2 \\
\rho \sigma_1 \sigma_2 & \sigma_2^2
\end{bmatrix}
$$
となる。
また、多次元ベクトルyに関しても、平均ベクトルと分散共分散行列を考えることで、確率密度関数を多変量に拡張することができて、
$$f_{\mathbf{Y}}(\mathbf{y}) = \frac{1}{(2\pi)^{n/2} |\det \Sigma|^{1/2}}
\exp \left( -\frac{1}{2} (\mathbf{y} – \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{y} – \boldsymbol{\mu}) \right)
$$
これに従う分布を多変量正規分布という。
カイ二乗分布
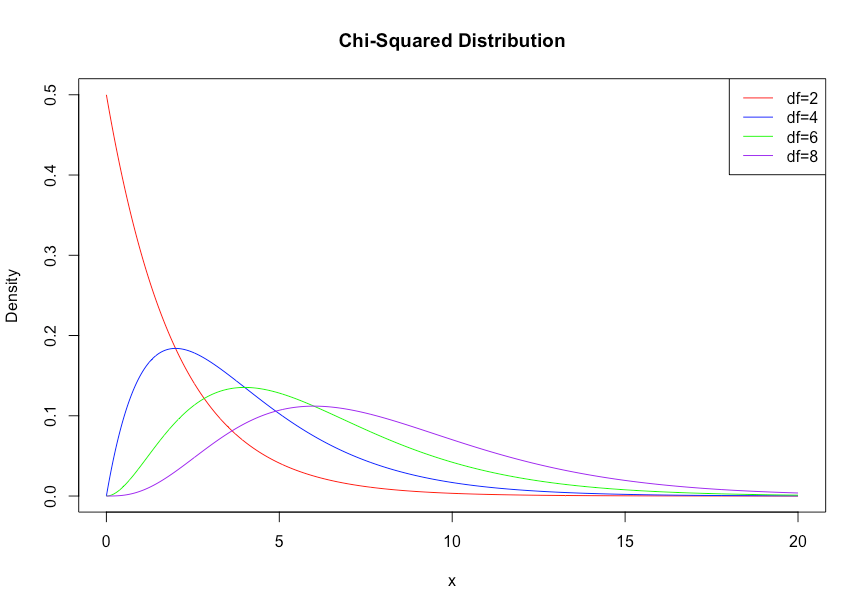
Z1,Z2,…..Zkを独立なN(0,1)に従う確率変数とする時、それらの2乗の和の分布を自由度kのカイ二乗分布という。
不偏標本分散を
$$S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i – \bar{X})^2$$
とする時、以下が成り立つ
$$\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$$
つまり、不偏標本分散から母分散を推定するときに、上記の統計量が自由度n-1のカイ二乗分布に従うことを利用できるということである。
さて、自由度nのカイ二乗分布の確率密度関数は
$$f_{\chi^2}(x) = \frac{1}{2^{n/2} \Gamma(n/2)} x^{(n/2)-1} e^{-x/2}, \quad x > 0$$
で示され、Ga(n/2, 1/2)と一致している。
また期待値はn、分散は2nとなる。
t分布
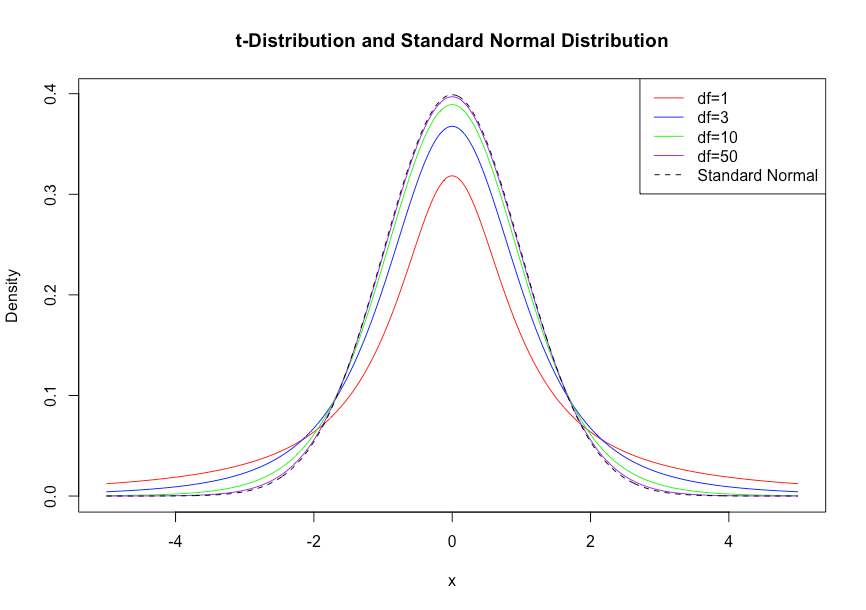
標本平均の標本分布は\(\mu, \frac{\sigma^2}{n}\)に従う(中心極限定理)
そしてその標準化\(z=\frac{\bar{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\)はN(0,1)に従う。
だが実際には母分散が既知であることは少ない。
そこで計算しやすい標本分散で母分散を代用して、このzもどきをtと呼ぶ。
すなわち、
$$t=\frac{\bar{X}-\mu}{\sqrt{\frac{s^2}{n}}}$$
である。
tは標準化でもなんでもないので、正規分布には従わない(n→∞であれば従う)
さて、そういえば前項で不偏分散と母分散で作られる統計量がカイ二乗分布に従うことが示されていて、それを変形すると
$$S^2 = \frac{\sigma^2}{n-1} \chi^2(n-1)$$
のようになる。これをtの式に代入して、
$$t = \frac{Z}{\sqrt{\frac{\chi^2(n-1)}{n-1}}}$$
となり、標準化変数とカイ二乗分布で表すことができ、これを自由度n-1のt分布という。
$$E[t] = 0 \quad (\text{for } n > 1)$$
$$\text{Var}[t] = \frac{n}{n-2}, \quad (n > 2)$$
となる。
F分布
2標本の標本平均の差の分布を考えるときに、母集団の分散が等しいかどうかで求める方法が異なる。
そこで母分散が等しいか調べるために、まずは標本分散を比べてみることにする。
2つの分散は独立として、カイ二乗分布に従うので、その比を統計量としたい。
今、確率変数UとVがそれぞれ独立にカイ二乗分布に従うとき、
フィッシャーの分散比
$$F = \frac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2}$$
を定義すると、 このFが従う分布を自由度(n1-1,n2-1)のF分布という。
ここで2つの母分散が等しければ、
$$F = \frac{S_1^2}{S_2^2}$$
となる。
まとめ
正規分布の確率密度関数:
$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x – \mu)^2}{2\sigma^2}\right)$$
指数分布の確率密度関数:
$$ f(x) = \begin{cases} \lambda e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases} $$
ガンマ分布の確率密度関数:
$$
f(x) = \frac{\lambda^\alpha x^{\alpha – 1} e^{-\lambda x}}{\Gamma(\alpha)}, \quad (x \geq 0)
$$
ベータ関数の確率密度関数:
$$
f(x) = \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{B(\alpha, \beta)}, \quad 0 \leq x \leq 1
$$
多変量正規分布の確率密度関数:
$$f_{\mathbf{Y}}(\mathbf{y}) = \frac{1}{(2\pi)^{n/2} |\det \Sigma|^{1/2}}
\exp \left( -\frac{1}{2} (\mathbf{y} – \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{y} – \boldsymbol{\mu}) \right)
$$
カイ二乗分布:
$$\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$$
t分布:
$$t = \frac{Z}{\sqrt{\frac{\chi^2(n-1)}{n-1}}}$$
F分布:
$$F = \frac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2}$$
今回は以上です!
長かった。。。


コメント