変数変換
連続確率変数Xの確率密度関数をf(x)とする
いま、新たな確率変数Y=g(X)を考える時、
Yの確率密度関数は
$$\frac{f(g^{-1}(y))}{|g'(g^{-1}(y))|}$$
※\(g^{-1}(x)\)は逆関数
で表せる。
例:自由度1、\(\chi^2\)分布の確率密度分布
標準正規分布に従う確率変数Xの確率密度関数は
$$f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$$
ここで、\(Y=X^2\)という確率変数(つまり\(\chi^2\)分布)を考えると、
その逆関数は\(X=\pm\sqrt{Y}\)となる。
そこで一旦X>0として、後で2倍することにする。
よって求める確率密度関数は、
$$2・\frac{\frac{1}{\sqrt{2\pi}} e^{-\frac{y}{2}}}{2\sqrt{y}}=\frac{1}{\sqrt{2\pi y}} e^{-\frac{y}{2}}$$
となる。
2変数の変数変換
2変数の同時確率密度関数をf(x,y)とする。
いま、変数変換\((z,w) = (u(x,y), v(x,y))\)という変換が1対1の変換であり、
逆変換\((x,y) = (s(u,v), t(u,v))\)が存在するとする。
変数変換(z,w)は行列では以下のように書ける。
$$
J =
\begin{bmatrix}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y}
\end{bmatrix}
$$
その行列式(ヤコビアン)は
$$
\det J = \frac{\partial u}{\partial x} \frac{\partial v}{\partial y} – \frac{\partial u}{\partial y} \frac{\partial v}{\partial x}
$$
したがって、変数変換後の確率密度関数は
$$
f_{Z,W}(z,w) = f_{X,Y}(x,y) \left| \frac{1}{\det J} \right|
$$
$$
f_{Z,W}(z,w) = f_{X,Y}(x,y) \left| \frac{1}{\frac{\partial u}{\partial x} \frac{\partial v}{\partial y} – \frac{\partial u}{\partial y} \frac{\partial v}{\partial x}} \right|
$$
ちなみにヤコビ行列のヤコビさんの本名はカール・グスタフ・ヤコブ・ヤコビさんらしいです。
データの変換
対数変換
人口、株価、所得など、一般に積が重なることで得られるデータは、
対数を取ることで正規分布に従う。
すなわち\(y=logx\)として、yの分布が正規分布に従う。
関数の性質上、x>0のデータに対して用いられる。
Box-Cox変換
べき乗変換\(y=x^a\)と対数変換を合わせたものとして、Box-Cox変換がある。
$$
y =
\begin{cases}
\frac{x^{\lambda} – 1}{\lambda}, & \text{if } \lambda \neq 0 \\
\log x, & \text{if } \lambda = 0
\end{cases}
$$
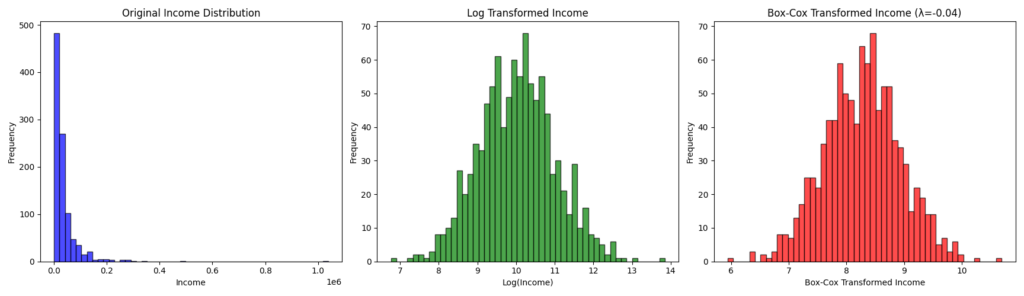
さて、pythonでは最適なパラメータλを勝手に計算してくれる(対数尤度が最大のものを採用する)ので、今回はλ=0.04が採用されています。
そのほかのλでの分布はこんな感じ、
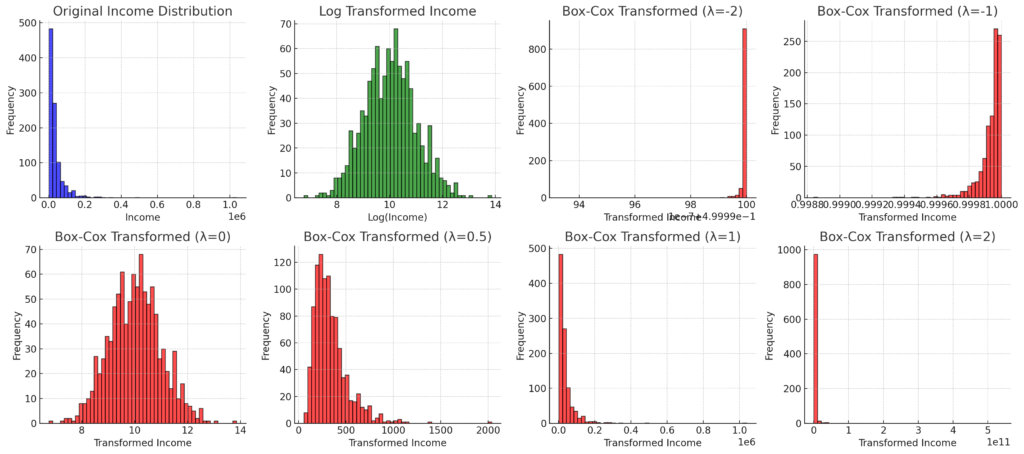
当たり前だけどλ=0の場合は対数変換と一致します。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# 1. 所得データのサンプルを生成(対数正規分布を使用)
np.random.seed(42)
income = np.random.lognormal(mean=10, sigma=1, size=1000) # 所得データ(大きめの値を想定)
# 2. 対数変換
log_income = np.log(income)
# 3. Box-Cox 変換(lambda を推定)
boxcox_income, lambda_bc = stats.boxcox(income)
# 4. ヒストグラムのプロット
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 変換前のデータ
axes[0].hist(income, bins=50, color='blue', alpha=0.7, edgecolor='black')
axes[0].set_title("Original Income Distribution")
axes[0].set_xlabel("Income")
axes[0].set_ylabel("Frequency")
# 対数変換後
axes[1].hist(log_income, bins=50, color='green', alpha=0.7, edgecolor='black')
axes[1].set_title("Log Transformed Income")
axes[1].set_xlabel("Log(Income)")
axes[1].set_ylabel("Frequency")
# Box-Cox 変換後
axes[2].hist(boxcox_income, bins=50, color='red', alpha=0.7, edgecolor='black')
axes[2].set_title(f"Box-Cox Transformed Income (λ={lambda_bc:.2f})")
axes[2].set_xlabel("Box-Cox Transformed Income")
axes[2].set_ylabel("Frequency")
plt.tight_layout()
plt.show()
Yeo-Johnson変換
さて、Box-Cox変換も、正のデータについてしか変換できないという欠点がある。
そこで負の値についても対応できるようにしたのがYeo-Johnson変換という。
しかしあまり使われていないらしいし、統計検定のテキストにも出てきてないので紹介に留めておく。
ロジット変換とロジスティック回帰
確率のような\(0 \leq p \leq 1\)の値をとるpを\(-\infty \leq p \leq \infty\)の範囲に変換するには
ロジット変換
$$y = log \frac{p}{1-p}$$
を用いる。
ちなみに、ここでy=ax+bとおいてpについて式変形すると、
$$p = \frac{1}{1+e^{-(ax+b)}}$$
となる。これはロジスティック回帰の回帰式である。
つまり、確率は本来0から1までの範囲しかとらないので、線形回帰できないが、ロジット変換で範囲を実数全体に変換できれば、線形回帰できるよね、っていうのがロジスティック回帰ということですね。
まとめ
変数変換:
確率変数Xの確率密度関数をf(x)に対して、確率変数Y=g(X)という変換を行う場合、
Yの確率密度関数は
$$\frac{f(g^{-1}(y))}{|g'(g^{-1}(y))|}$$
※\(g^{-1}(x)\)は逆関数
2変数の変数変換:
$$
f_{Z,W}(z,w) = f_{X,Y}(x,y) \left| \frac{1}{\det J} \right|
$$
なお、
$$
\det J = \frac{\partial u}{\partial x} \frac{\partial v}{\partial y} – \frac{\partial u}{\partial y} \frac{\partial v}{\partial x}
$$
対数変換:
\(y=logx\)
Box-Cox変換:
$$
y =
\begin{cases}
\frac{x^{\lambda} – 1}{\lambda}, & \text{if } \lambda \neq 0 \\
\log x, & \text{if } \lambda = 0
\end{cases}
$$
ロジット変換:
$$y = log \frac{p}{1-p}$$
本日はここまで。最後のロジスティック回帰の部分に関しては改めて考えるとなるほどなって感じでした。


コメント