今回は確率関数と母関数についてです。
累積分布関数
確率変数Xに対して、xと実数とするとき、
$$F(X) = P(X \leq x)$$
をXの累積密度関数という
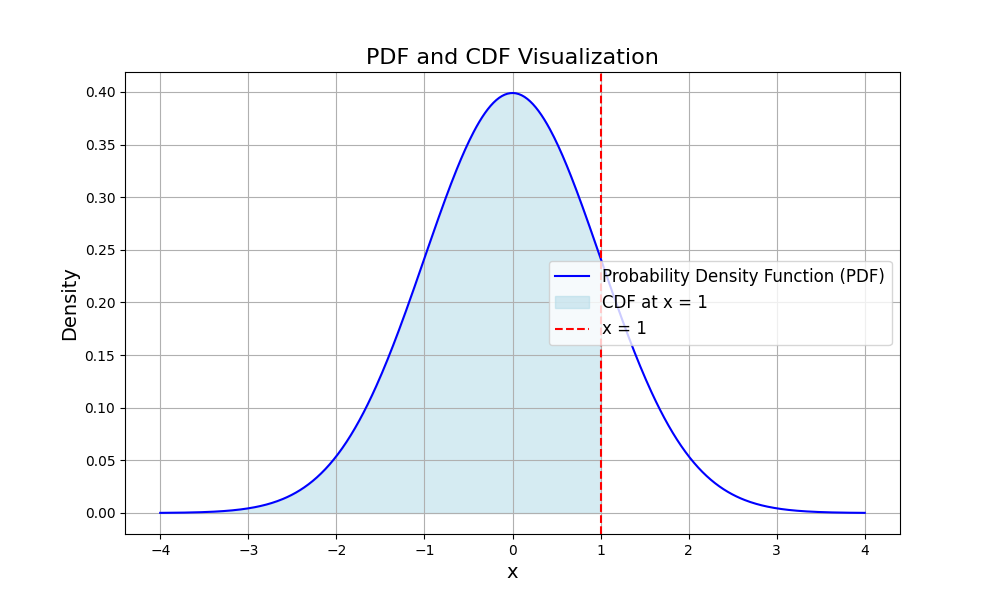
指数関数の場合は
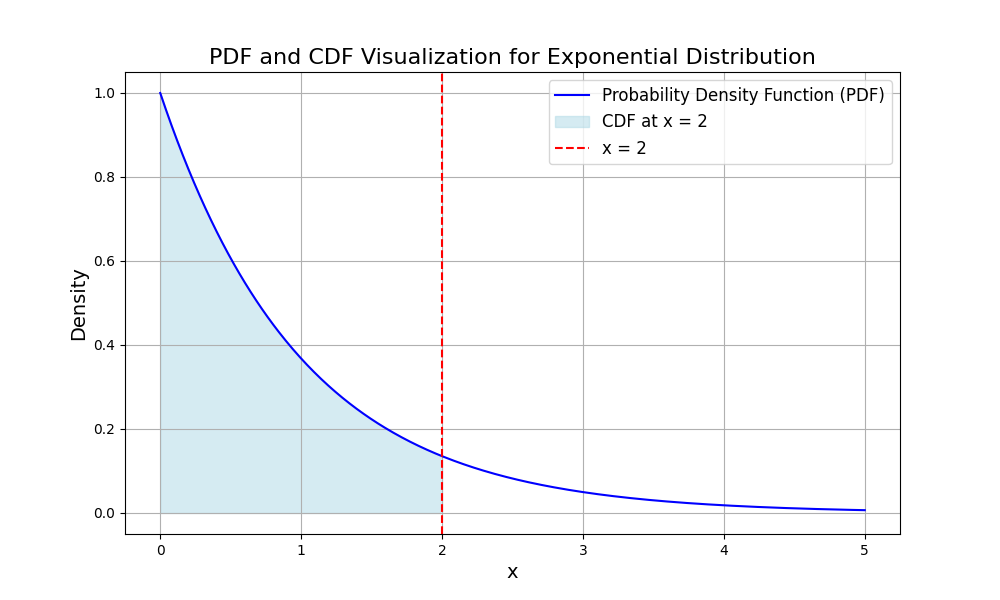
この時、S(X)=1-F(x)、つまり赤線の右側を生存関数という。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Define the range and parameters for the normal distribution
x = np.linspace(-4, 4, 500)
mean = 0
std_dev = 1
# Compute the PDF and CDF
pdf = norm.pdf(x, mean, std_dev) #指数関数はexpon
cdf = norm.cdf(x, mean, std_dev)
# Choose a point x0
x0 = 1
# Plot the PDF
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="Probability Density Function (PDF)", color="blue")
# Fill the area under the PDF up to x0
x_fill = np.linspace(-4, x0, 500)
y_fill = norm.pdf(x_fill, mean, std_dev)
plt.fill_between(x_fill, y_fill, color="lightblue", alpha=0.5, label=f"CDF at x = {x0}")
# Mark x0
plt.axvline(x=x0, color="red", linestyle="--", label=f"x = {x0}")
# Add labels, legend, and title
plt.title("PDF and CDF Visualization", fontsize=16)
plt.xlabel("x", fontsize=14)
plt.ylabel("Density", fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
# Show the plot
plt.show()同時確率分布と周辺確率分布
2つの連続確率変数X, Yに関してX=xかつY=yである確率
$$P(X=x, Y=y)=f(x,y)$$
を2次元確率変数の同時確率分布という。
ここで、
$$f(x,y) \leq 0$$
$$\int \int f_{X,Y}(x, y) \; dx \; dy =1 $$
である。この時にX, Y単独の確率分布は、
$$g(x) = \int f_{X,Y}(x, y) \; dy $$
$$h(y) = \int f_{X,Y}(x, y) \; dx $$
であり、これをX, Yの周辺確率分布という。
同時確率分布から周辺確率分布を求めることはできるが、周辺確率分布から同時確率分布を求めることはできない。
条件付き確率関数
X=xが確定した場合ににY=yとなる条件付き確率は
$$P_{Y|X} (y|x) = \frac{f(x,y)}{g(x)}$$
で表される。
モーメント母関数
確率分布の形を代表する値(特性値)には、期待値、中央値、etc…様々なものがあるが、
それらを代表する関数があれば便利である。
期待値、分散、歪度、尖度など、それぞれの特性値はいずれも、
$$\mu _r = E(X – \mu)^r$$
の形が含まれている。
これを期待値周りのr次モーメントという。
つまり、すべてのrについてモーメントを指定できれば、一つの確率変数の分布を表すことができるはずである。
これをモーメント母関数といい、
$$M_{x}(t) = E(e^{tx})$$
と定義する。
モーメント母関数を微分してt=0とすると、各次のモーメントがわかる。
すなわち
$$M_{x}'(0)=\mu _1, M_{x}”(0)=\mu _2$$
これは\(e^{tx}\)をテイラー展開すれば微分すると低次項が消え、t=0とすると高次項が消えることがわかる。
$$f(x) = f(a) + f'(a)(x-a) + \frac{1}{2!}f^{\prime\prime}(a)(x-a)^{2} + \frac{1}{2!}f^{\prime\prime\prime}(a)(x-a)^{3} + …$$
$$x(u + \Delta u)をuまわりでテイラー展開すると$$
$$x(u + \Delta u) = x(u) + f'(u)((u + \Delta u) -u) + \frac{1}{2!}f^{\prime\prime}(u)((u + \Delta u) -u)^{2} + \frac{1}{2!}f^{\prime\prime\prime}(u)(u + \Delta u) -u)^{3} + …$$
$$x(u + \Delta u) = x(u) + f'(u)(\Delta u) + \frac{1}{2!}f^{\prime\prime}(u)(\Delta u)^{2} + \frac{1}{2!}f^{\prime\prime\prime}(u)(\Delta u)^{3} + …$$
二次項以降は近似して
$$x(u + \Delta u) \simeq x(u) + f'(u)(\Delta u)$$
例として、標準正規分布のモーメント母関数はこちら
確率変数の和のモーメント
独立な確率変数\(X_1, X_2\)について、そのモーメント母関数を\(m_{1}(\theta), m_{2}(\theta)\)とするとき、
確率変数\(X_1 + X_2\)のモーメント母関数は\(m_{1}(\theta)m_{2}(\theta)\) となる。
今回は以上です!


コメント